Na figura, o circuito consiste de uma bateria de tensão conectada a um capacitor de placas paralelas, de área e distância entre si, dispondo de um dielétrico de permissividade elétrica que preenche completamente o espaço entre elas.
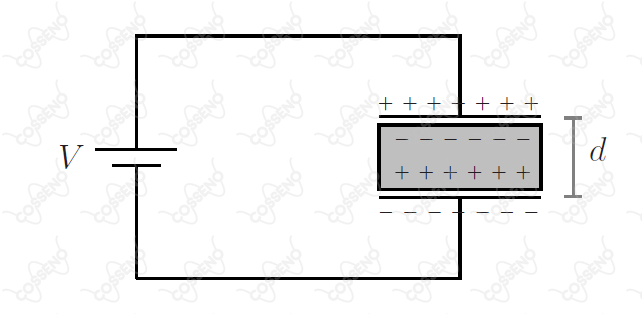
Assinale a magnitude da carga induzida sobre a superfície do dielétrico.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pensando na presença do dielétrico, vale voltar visualizar a imagem um instante. Verifique que a presença dele induz uma carga na superfície do dielétrico, esta que irá produzir um campo induzido contrário ao $E_{total}$ (campo produzido pelas placas), ou seja, o campo elétrico resultante terá menor magnitude, sendo ele:\begin{matrix}E_{resultante} = E_{total} - E_{induzido}
\end{matrix}Assim, conhecido o conceito de densidade superficial de carga, sabe-se que:\begin{matrix}
E = \dfrac{\sigma}{\varepsilon} &,& \sigma = \dfrac{Q}{S}
\end{matrix}Então, conforme campo elétrico resultante:\begin{matrix}
\dfrac{Q_{resultante}}{S \varepsilon} = \dfrac{Q_{total}}{S\varepsilon} - \dfrac{q}{S\varepsilon}
\end{matrix}$\color{orangered}{\text{Obs:}}$ Como em ambas as situações - com e sem o dielétrico - o capacitor está exposto a mesma diferença de potencial, o campo elétrico $E_{resultante}$ deve permanecer constante. Portanto, a carga resultante é igual a carga inicial sem o dielétrico.\begin{matrix}
q = Q_{total} - Q_{resultante}
\end{matrix}Conhecido os conceitos de capacitância, sabemos:\begin{matrix}
C = \dfrac{\varepsilon S}{d} &,& Q = CV
\end{matrix}Então,\begin{matrix}
q = \dfrac{\varepsilon S}{d}V -\dfrac{\varepsilon_0 S}{d}V
\end{matrix}Portanto,\begin{matrix}\boxed{q = \dfrac{SV}{d}(\varepsilon - \varepsilon_0) }
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

