A princípio, sabemos que a distância entre $A$ e $B$ é a aresta de um cubo circunscrito a um octaedro. Nesse sentido, podemos encontrar o comprimento desta aresta a partir da distância euclidiana:\begin{matrix} (\overline{AB})^2 = (3-4)^2 + (4-3)^2 &\therefore& \overline{AB} = \sqrt{2} \end{matrix}Conforme enunciado, queremos a área lateral do octaedro inscrito, este que sabemos possuir os vértices nos pontos médios da face do cubo. Com isso, você pode tentar esboçar a situação ou já ter a figura prévia em mente. Contudo, há também outra forma de tratar o problema, talvez a mais rudimentar da matemática, que é a simplificação. Note que o octaedro descrito não é nada mais do que a perfeita junção de duas pirâmides de bases quadradas, estas que apresentam mesma altura $\sqrt{2}/2$. Veja abaixo a situação: 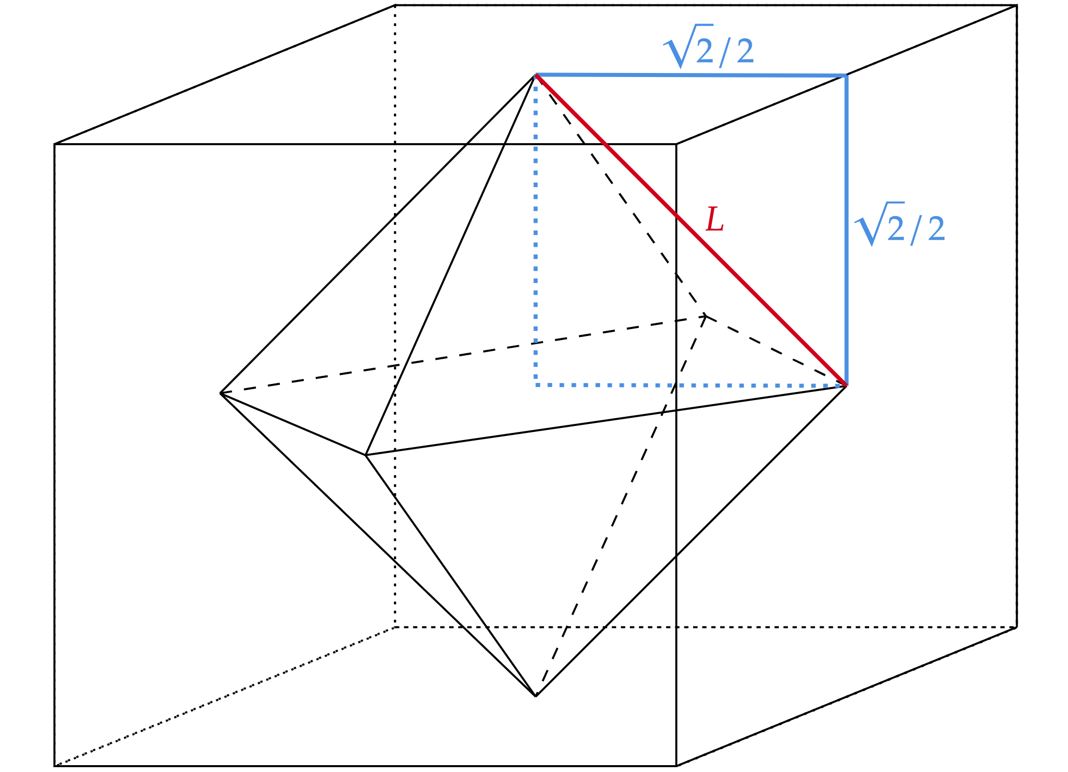Não é difícil encontrar $L$, pelo teorema de Pitágoras:\begin{matrix} L^2 = \left( \dfrac{\sqrt{2}}{2}\right)^2 + \left( \dfrac{\sqrt{2}}{2}\right)^2 &\therefore& L =1 \end{matrix}A partir disso, já é possível calcular a área lateral solicitada, visto que o octaedro em questão é dual, ou seja, regular. No entanto, você também poderia olhar para base da pirâmide em análise: 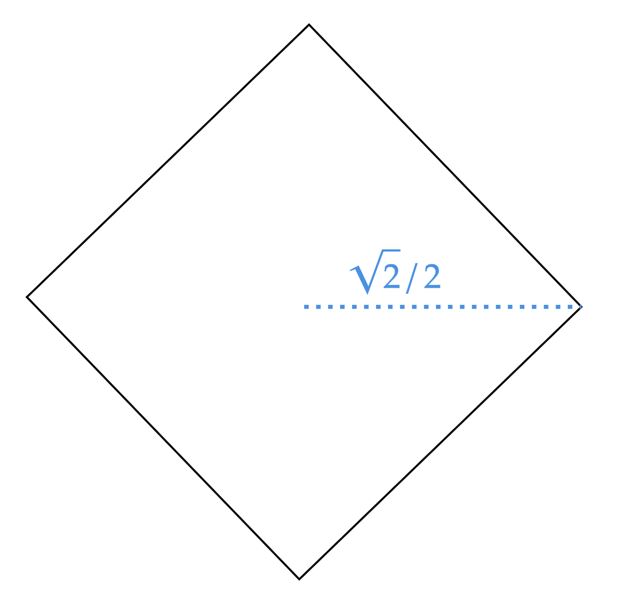Dessa forma, é notório que a aresta da base também é $L$. Adiante, calculando a área lateral do octaedro, podemos calcular a área de $8$ triângulos equiláteros de lado $1$, o que equivale a área lateral das duas pirâmides citadas:\begin{matrix} A = 8 \cdot \left(\dfrac{L^2\sqrt{3}}{4}\right) &\therefore& A = \sqrt{12} \end{matrix}\begin{matrix}Letra \ (C) \end{matrix}