A princípio, podemos esboçar a figura de forma grosseira no viés de entender o problema de forma qualitativa, e não tão analítica como se espera. (Claro que iremos fazer isso sem perda de generalidade.) Veja: 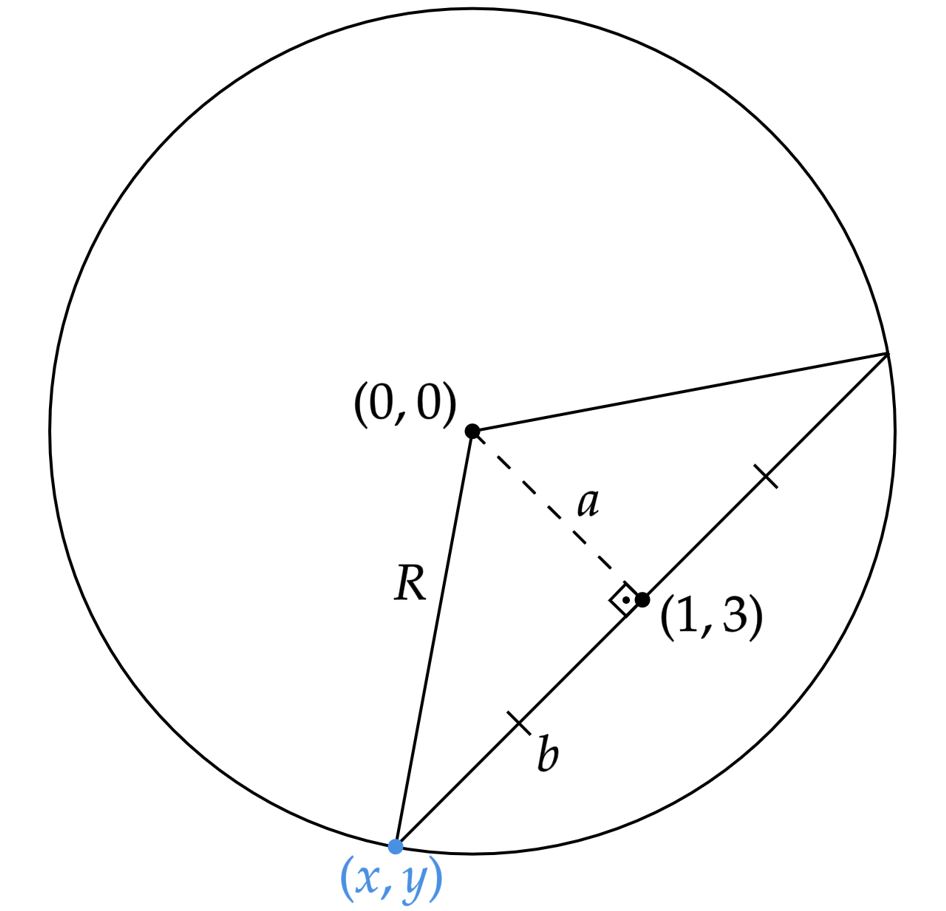A partir daqui existem diversas formas de resolver o problema: $• \ \text{Resolução I:}$ $\color{#3368b8}{\text{Distância Euclidiana}}$ Com o conhecimento da distância entre dois pontos é possível resolver o problema, a princípio, vamos tentar encontrar $a$:\begin{matrix} a^2 = (1-0)^2 + (3-0)^2 &\therefore& a = \sqrt{10} \end{matrix}Segundo o teorema de Pitágoras:\begin{matrix} R^2 = a^2 + b^2 \end{matrix}Aplicando a distância euclidiana entre o ponto médio e o ponto $(x,y)$, assim como entre o centro e ponto $(x,y)$ que pertence a reta:\begin{align} R^2 &= (x-0)^2 + (y-0)^2 \\ b^2 &= (x-1)^2 + (y-3)^2 \end{align}Então, substituindo os resultados no teorema de Pitágoras:\begin{matrix} x^2 + y^2 = (x-1)^2 + (y-3)^2 + 10 \end{matrix}\begin{matrix}\boxed{3y + x - 10 = 0} \end{matrix}$• \ \text{Resolução II:}$ $\color{#3368b8}{\text{Coeficiente angular}}$ Observe que a reta que passa entre o centro e o ponto médio é perpendicular a reta que contém $\overline{AB}$. Com isso, sabemos que se o coeficiente angular de uma for $r$ e da outra $s$, deve-se ter:\begin{matrix} r \cdot s = -1 \end{matrix}Assim, encontrando o coeficiente angular da reta que passa pelo centro e pelo ponto médio, têm-se:\begin{matrix} r = \dfrac{3-0}{1-0} &\therefore& r = 3 \end{matrix}Consequentemente, $s = -1/3$, ou seja:\begin{matrix}- \dfrac{1}{3} = \dfrac{y-3}{x-1} &\therefore& \boxed{3y + x - 10 = 0} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}