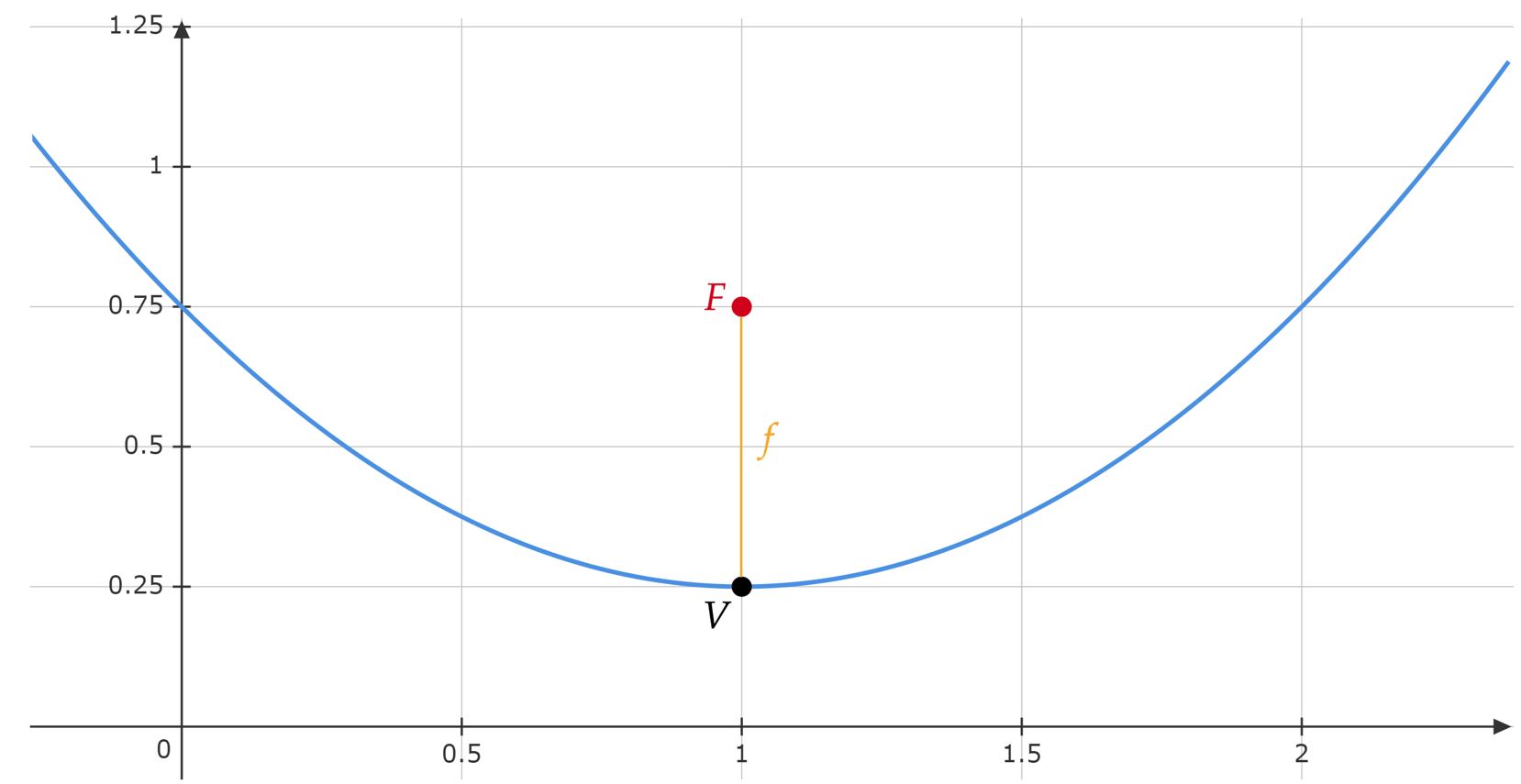
A princípio, vamos tentar encontrar a equação reduzida desta parábola, esta que deve ser na forma:\begin{matrix} (x - x_v)^2 = 4f(y - y_v) &,& \text{distância entre o foco e o vértice} :=f \end{matrix}Com isso, têm-se conforme enunciado:\begin{align} 2(x^2 -2x +1) + 1 -4y &= 0 \\ 2(x-1)^2 &= 4y -1 \\ (x-1)^2 &= 2\left(y -\dfrac{1}{4}\right) \end{align}Assim,\begin{matrix}4f = 2 &\therefore& f = \dfrac{1}{2} & \tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (E) \end{matrix}

Pensando na parábola como uma equação de segundo grau, temos: $$ y = \frac{x^2}{2} - x + \frac{3}{4} $$ Pensando na forma $$ y = a.x^2 + b.x + c $$ Temos que $$ a = \frac{1}{2} \ , \ b = -1 \ , \ c = \frac{3}{4} $$ Sabendo que a excentricidade da parábola é sempre igual a 1, temos: $$ e = \frac{f}{a} = 1 \Rightarrow f = a = \frac{1}{2} $$