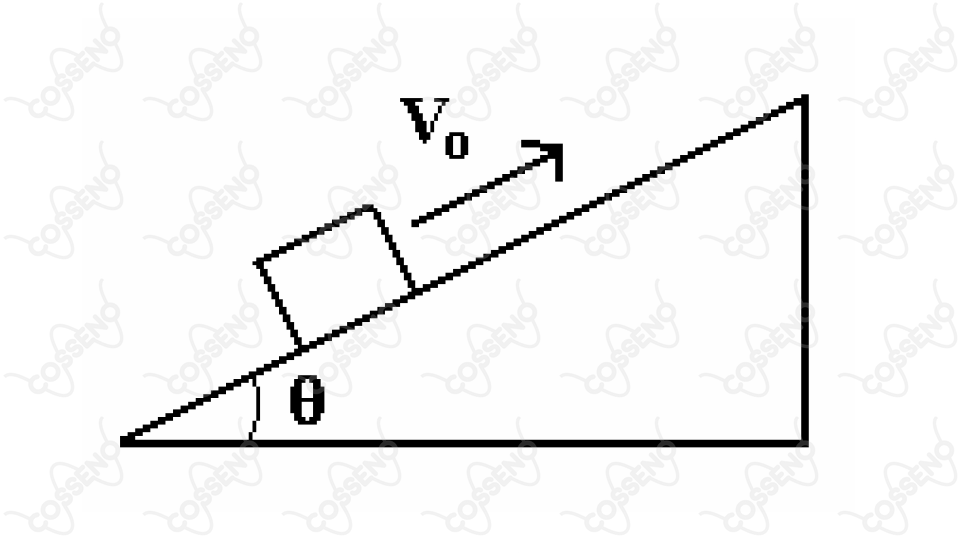
Na figura, um bloco sobe um plano inclinado, com velocidade inicial . Considere ο coeficiente de atrito entre o bloco e a superfície. Indique a sua velocidade na descida ao passar pela posição inicial.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, pode-se analisar as forças que atuam no bloco em dois momentos, um momento na subida, e outro na descida. Na subida, o impulso inferido ao bloco é responsável por seu movimento, este que deve ser contrário à força peso, assim como o atrito. Contudo, na descida a situação é diferente, o bloco parte do repouso a partir da contribuição da força peso, enquanto novamente o atrito contraria o movimento. Nesse contexto, pode-se esboçar os dois momentos como:
 Decompondo as forças peso, assim como admitindo o movimento para cima e para direita como positivos, têm-se:
$• \ \text{Subida:}$ Vamos começar encontrando a aceleração que atua no bloco, e em seguida aplicar Torricelli a fim de relacionar a velocidade até o ponto máximo de subida - momento em que o bloco para.\begin{matrix} F = - P - F_{at} \\
ma_0 = -mg\sin{\theta} - \mu mg\cos{\theta} \\ \boxed{a_0 = -g(\sin{\theta} + \mu \cos{\theta} )}
\end{matrix}Por Torricelli:\begin{matrix}
0^2 = V^2_0 + 2a_0L \\
\boxed{V^2_0 = 2g(\sin{\theta} + \mu \cos{\theta} )L} \ \ (1)
\end{matrix}$\color{orangered}{\text{Obs:}}$ $L$ é a distância que o bloco percorreu na rampa.
$• \ \text{Descida:}$ O raciocínio é análogo ao anterior, note que agora o bloco parte do repouso, assim como deve percorrer uma mesma distância $L$, afinal, ele está fazendo o mesmo trajeto, mas no sentido contrário:\begin{matrix} F = P - F_{at} \\
ma = mg\sin{\theta} - \mu mg\cos{\theta} \\ \boxed{a = g(\sin{\theta} - \mu \cos{\theta} )}
\end{matrix}Por Torricelli:\begin{matrix}
V^2 = 0^2 + 2aL \\
\boxed{V^2= 2g(\sin{\theta} - \mu \cos{\theta} )L} \ \ (2)
\end{matrix}Racionalizando $(1)$ e $(2)$, facilmente constatamos:\begin{matrix}
V = V_0 \sqrt{\dfrac{\sin{\theta} - \mu \cos{\theta}}{\sin{\theta} +\mu \cos{\theta}}} \ \ \ \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}
Decompondo as forças peso, assim como admitindo o movimento para cima e para direita como positivos, têm-se:
$• \ \text{Subida:}$ Vamos começar encontrando a aceleração que atua no bloco, e em seguida aplicar Torricelli a fim de relacionar a velocidade até o ponto máximo de subida - momento em que o bloco para.\begin{matrix} F = - P - F_{at} \\
ma_0 = -mg\sin{\theta} - \mu mg\cos{\theta} \\ \boxed{a_0 = -g(\sin{\theta} + \mu \cos{\theta} )}
\end{matrix}Por Torricelli:\begin{matrix}
0^2 = V^2_0 + 2a_0L \\
\boxed{V^2_0 = 2g(\sin{\theta} + \mu \cos{\theta} )L} \ \ (1)
\end{matrix}$\color{orangered}{\text{Obs:}}$ $L$ é a distância que o bloco percorreu na rampa.
$• \ \text{Descida:}$ O raciocínio é análogo ao anterior, note que agora o bloco parte do repouso, assim como deve percorrer uma mesma distância $L$, afinal, ele está fazendo o mesmo trajeto, mas no sentido contrário:\begin{matrix} F = P - F_{at} \\
ma = mg\sin{\theta} - \mu mg\cos{\theta} \\ \boxed{a = g(\sin{\theta} - \mu \cos{\theta} )}
\end{matrix}Por Torricelli:\begin{matrix}
V^2 = 0^2 + 2aL \\
\boxed{V^2= 2g(\sin{\theta} - \mu \cos{\theta} )L} \ \ (2)
\end{matrix}Racionalizando $(1)$ e $(2)$, facilmente constatamos:\begin{matrix}
V = V_0 \sqrt{\dfrac{\sin{\theta} - \mu \cos{\theta}}{\sin{\theta} +\mu \cos{\theta}}} \ \ \ \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

Ampliar Imagem
Seja $g$ a gravidade , $a_{s}$ a aceleração do bloco na subida , $a_{d}$ a aceleração do bloco na decida ,$V_{f}$ a velocidade do bloco na descida ao passar pela posição inicial , $S$ a distância máxima percorrida pelo bloco na subida , $m$ a massa do bloco , $P$ o peso do bloco e $f_{at}$ a força de atrito entre o bloco e a superfície.
Analisando o bloco durante a subida poderemos encontrar as seguintes relações :
$m\cdot a_{s} = f_{at} + P\cdot \sin(\theta) $ $\land$ $ (V_{0})^2-2a_{s}\cdot S =0 $
Desenvolvendo essas equações teremos que
$ (V_{0})^2-2a_{s}\cdot S =0 \implies S = \dfrac{(V_{0})^2}{2a_{s}}$
$m\cdot a_{s} = f_{at} + P\cdot \sin(\theta) = m\cdot a_{s} = \mu mg \cdot \cos(\theta) + mg \cdot \sin(\theta) $
$\implies a_{s} = g \cdot \sin(\theta) + \mu g \cdot \cos(\theta) $
$=a_{s} = g (\sin(\theta) + \mu \cdot \cos(\theta)) $
$\therefore$
$S = \dfrac{(V_{0})^2}{2a_{s}}$
$= \boxed{S = \dfrac{(V_{0})^2}{2g (\sin(\theta) + \mu \cdot \cos(\theta))}}$
Agora Iremos analisar o bloco durante a descida , realizando essa análise poderemos encontrar as seguintes igualdades:
$m \cdot a_{d} = P \cdot \sin(\theta) - f_{at} $ $\land$ $(V_{f})^2 = 2a_{d} \cdot S$
Desenvolvendo as igualdades teremos que
$(V_{f})^2 = 2a_{d} \cdot S \implies S = \dfrac{(V_{f})^2}{2a_{d}}$
$m \cdot a_{d} = P \cdot \sin(\theta) - f_{at} = m \cdot a_{d} = mg \cdot \sin(\theta) - \mu mg \cdot \cos(\theta) $
$\implies a_{d} = g \cdot \sin(\theta) - \mu g \cdot \cos(\theta) =
a_{d} = g(\sin(\theta) - \mu \cdot \cos(\theta)) $
$\therefore$
$S = \dfrac{(V_{f})^2}{2a_{d}}$
$= \boxed{S = \dfrac{(V_{f})^2}{2g(\sin(\theta) - \mu \cdot \cos(\theta))}}$
$\therefore$
$\dfrac{(V_{f})^2}{2g(\sin(\theta) - \mu \cdot \cos(\theta))}=\dfrac{(V_{0})^2}{2g (\sin(\theta) + \mu \cdot \cos(\theta))} $
$\implies (V_{f})^2 =(V_{0})^2 \cdot \left(\dfrac{\sin(\theta) - \mu \cdot \cos(\theta)}{\sin(\theta) + \mu \cdot \cos(\theta)}\right) $
$\implies \boxed{V_{f} =V_{0} \cdot \sqrt{\dfrac{\sin(\theta) - \mu \cdot \cos(\theta)}{\sin(\theta) + \mu \cdot \cos(\theta)}}} $
$\textbf{Resposta : Alternativa B}$



