A figura mostra uma bobina com espiras de de área e de resistência. Uma indução magnética de teslas é inicialmente aplicada ao longo do plano da bobina. Esta é então girada de modo que seu plano perfaça um ângulo de em relação à posição inicial. Nesse caso, qual o valor da carga elétrica que deve fluir pela bobina?
CossenoGPT
Teste
gratuitamente agora
mesmo! 
A princípio, podemos pensar na $\text{lei de Lenz-Faraday}$, em que para $N$ espiras, têm-se:\begin{matrix}
|\varepsilon| = N\dfrac{\Delta \Phi}{\Delta t}
\end{matrix}Conforme enunciado, conseguirmos analisar o fluxo magnético em cada situação: final e inicial. Nessa perspectiva, inicialmente não temos fluxo magnético, visto que o campo magnético é paralelo ao plano da bobina. Adiante, na situação final, constatamos fluxo, este que pode ser representado como:\begin{matrix}
\Phi_{final} = BA\cos{60º}
\end{matrix}Rotacionando a situação, verifica-se algo como:
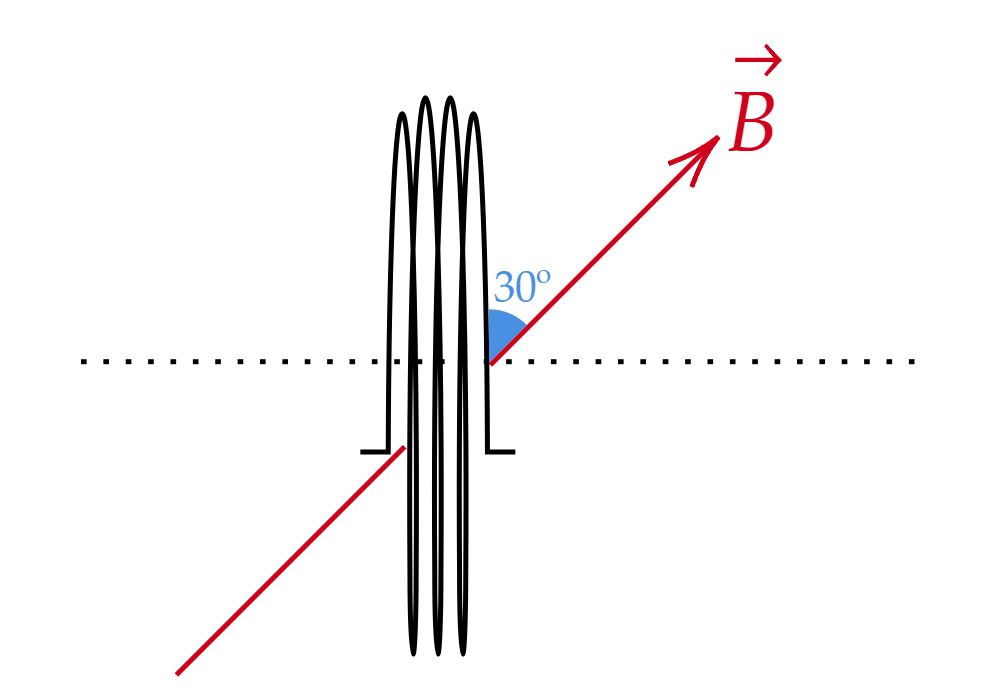Substituindo os resultados,\begin{matrix}
|\varepsilon| = N \dfrac{BA\cos{60º}}{\Delta t}
\end{matrix}Pela $\text{primeira lei de Ohm}$:\begin{matrix}
R\cdot i= N \dfrac{BA\cos{60º}}{\Delta t}
\end{matrix}Conhecido o conceito de corrente, isto é:\begin{matrix} i = \dfrac{Q}{\Delta t}
\end{matrix}Constata-se:\begin{matrix}
RQ = N BA\cos{60º} \\
40 Q = 80 \cdot 4 \cdot 0,5 \cdot \dfrac{1}{2}
\end{matrix}\begin{matrix}\boxed{Q = 2,0 \ \pu{C}}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}
Ampliar Imagem
