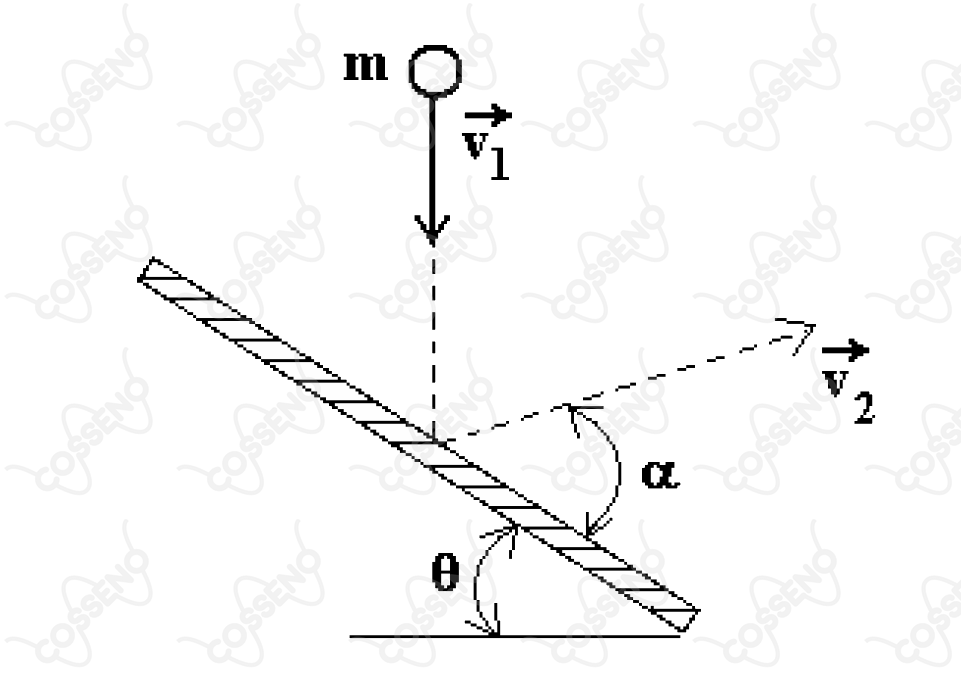
A figura mostra uma bola de massa que cai com velocidade sobre a superfície de um suporte rígido, inclinada de um ângulo em relação ao plano horizontal. Sendo o coeficiente de restituição para esse impacto, calcule o módulo da velocidade com que a bola é ricocheteada, em função de , e . Calcule também o ângulo .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$1)$ Utilizando coeficiente de restituição para obter alguma relação interessante:
$$e = \dfrac{V_{afastamento}}{V_{aproximação}} = \dfrac{V_{2}\sin \alpha}{V_{1}\cos \theta} \Rightarrow \sin \alpha = \dfrac{V_{1}\cos \theta \cdot e}{V_{2}} \ (1)$$
$2)$ Pode-se obter outra relação a partir da análise da direção paralela ao plano inclinado.
$$V_{1}\sin \theta = V_{2}\cos \alpha \Rightarrow \cos \alpha = \dfrac{V_{1}\sin \theta}{V_{2}} \ (2)$$
$3)$ Para encontrar $\vec{V}_{2}$ basta utilizar a relação fundamental da trigonometria em $\alpha$, perceba que malandramente isolei $\alpha$ para sumir e obter algo em função de $\theta$.
$$\sin^{2} \alpha + \cos^{2} \alpha = 1 \Rightarrow \dfrac{\vert \vec{V}_{1} \vert^{2} \cos^{2} \theta \cdot e ^{2}}{\vert \vec{V}_{2} \vert^{2}} + \dfrac{\vert \vec{V}_{1} \vert^{2} \sin^{2} \theta}{\vert \vec{V}_{2} \vert^{2}} = 1 $$
$$\vert \vec{V}_{2}\vert = \vert \vec{V}_{1} \vert \cdot \sqrt{e^{2}\cos^{2} \theta + \sin^{2} \theta}.$$
$4)$ Para encontrar $\alpha$ basta fazer $(1) \div (2)$.
$$\alpha = \arctan (e \cdot \cotg \theta).$$

