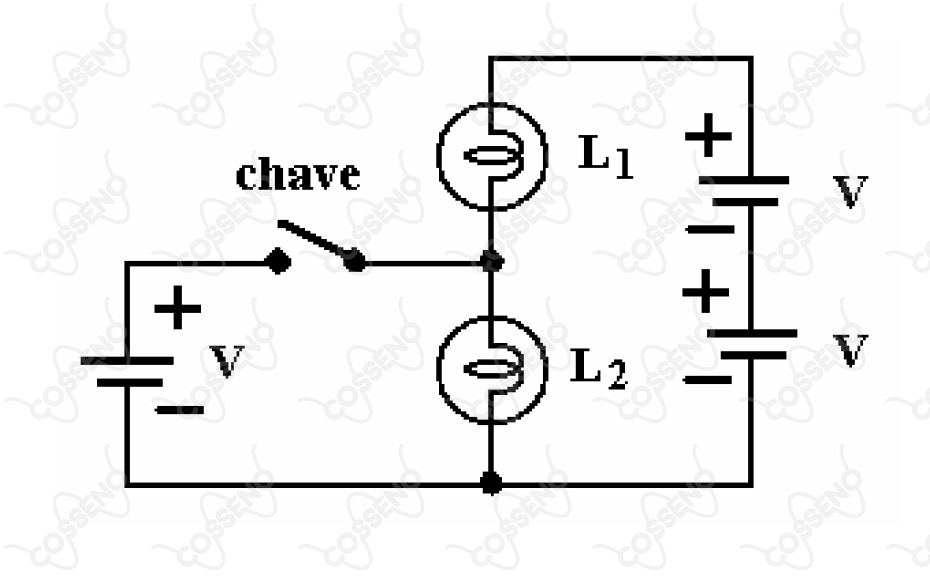
No circuito representado na figura, têm-se duas lâmpadas incandescentes idênticas, e , e três fontes idênticas, de mesma tensão . Então, quando a chave é fechada
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Admitindo que as baterias são ideais, vamos começar analisando o circuito com a chave aberta:
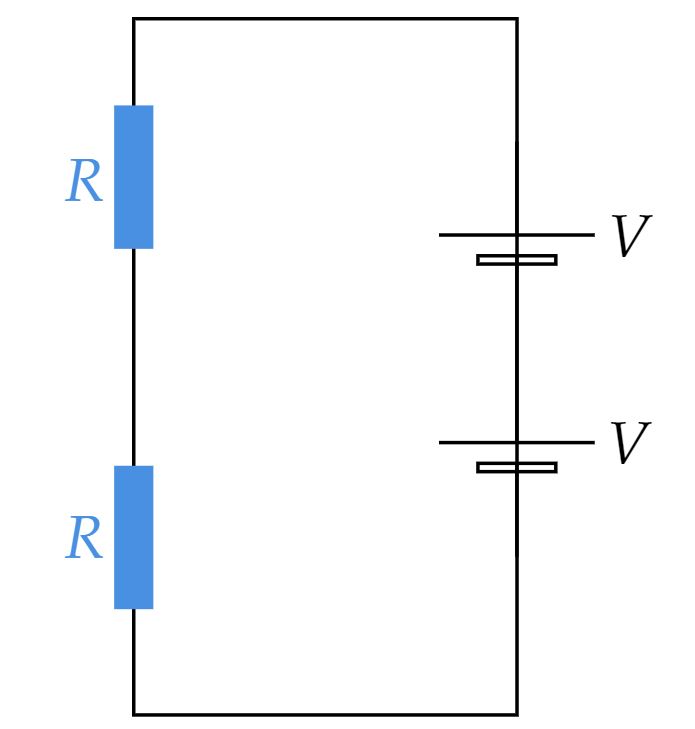 Pela primeira lei de Ohm, têm-se:\begin{matrix} 2V =2R \cdot i_a &\therefore&V = R \cdot i_a
\end{matrix}Com isso, verificamos que cada lâmpada de resistência $R$ está exposta a uma tensão $V$. Agora, pensando no circuito com a chave fechada, repare que a lâmpada $L_2$ está sujeita a uma tensão $V$ devido a bataria da esquerda. Nesse sentido, pela primeira lei de Ohm para lâmpada $L_2$:\begin{matrix}
V = R \cdot i_2 &\therefore& i_2 = i_a
\end{matrix}Desse modo, o brilho na lâmpada $2$ deve permanecer o mesmo, afinal, a tensão e a corrente são as mesmas - então a potência dissipada no resistor é idêntica. Analogamente, pensando em $L_1$, também constatamos uma diferença de potencial $V$, veja:
Pela primeira lei de Ohm, têm-se:\begin{matrix} 2V =2R \cdot i_a &\therefore&V = R \cdot i_a
\end{matrix}Com isso, verificamos que cada lâmpada de resistência $R$ está exposta a uma tensão $V$. Agora, pensando no circuito com a chave fechada, repare que a lâmpada $L_2$ está sujeita a uma tensão $V$ devido a bataria da esquerda. Nesse sentido, pela primeira lei de Ohm para lâmpada $L_2$:\begin{matrix}
V = R \cdot i_2 &\therefore& i_2 = i_a
\end{matrix}Desse modo, o brilho na lâmpada $2$ deve permanecer o mesmo, afinal, a tensão e a corrente são as mesmas - então a potência dissipada no resistor é idêntica. Analogamente, pensando em $L_1$, também constatamos uma diferença de potencial $V$, veja:
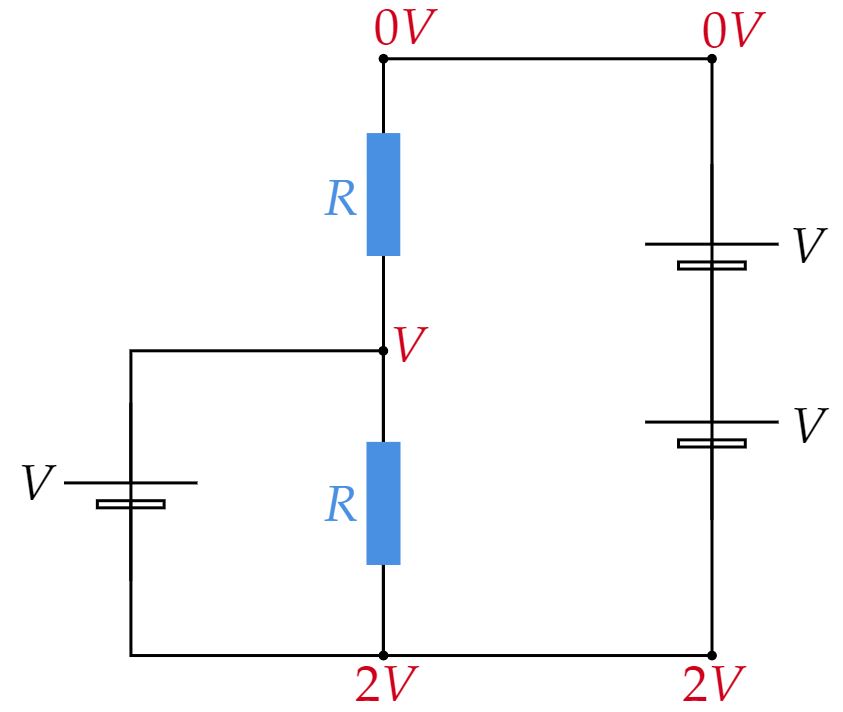 O raciocínio segue pela primeira lei de Ohm:\begin{matrix}
V = R \cdot i_1 &\therefore& i_1 = i_2 = i_a
\end{matrix}Portanto, ambas as lâmpadas permanecem com o mesmo brilho.\begin{matrix}Letra \ (E)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Assumindo que as baterias não eram ideais, o resultado seria diferente, no caso, ambas as lâmpadas arriariam o brilho. Contudo, não há essa opção como resposta, ou seja, elas precisam ser ideais a fim de chegar num resultado apropriado.
O raciocínio segue pela primeira lei de Ohm:\begin{matrix}
V = R \cdot i_1 &\therefore& i_1 = i_2 = i_a
\end{matrix}Portanto, ambas as lâmpadas permanecem com o mesmo brilho.\begin{matrix}Letra \ (E)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Assumindo que as baterias não eram ideais, o resultado seria diferente, no caso, ambas as lâmpadas arriariam o brilho. Contudo, não há essa opção como resposta, ou seja, elas precisam ser ideais a fim de chegar num resultado apropriado.

Ampliar Imagem

Ampliar Imagem

