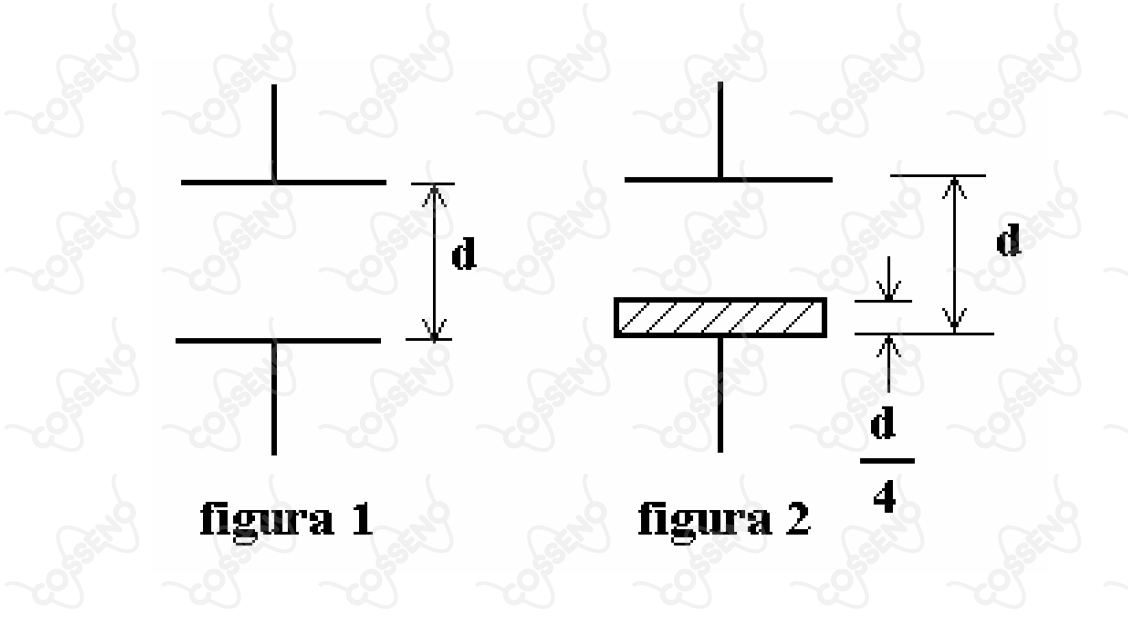
A figura mostra um capacitor de placas paralelas com vácuo entre as placas, cuja capacitância é . Num determinado instante, uma placa dielétrica de espessura e constante dielétrica é colocada entre as placas do capacitor, conforme a figura . Tal modificação altera a capacitância do capacitor para um valor . Determine a razão .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, deve-se ter conhecimento que:\begin{matrix}
C = \dfrac{\varepsilon_0 A}{d} &,& K = \dfrac{\varepsilon}{\varepsilon_0}
\end{matrix}Para a situação inicial, têm-se:\begin{matrix}
C_0 = \dfrac{\varepsilon_0 A}{d}
\end{matrix}Já para segunda situação, nós temos a formação de dois capacitores em série, um com permissividade $\varepsilon_0$ e outro com permissividade $K\varepsilon_0$, vamos denotá-los, respectivamente, pelos índices $x$ e $y$:\begin{matrix}
C_x = \dfrac{\varepsilon_0 A}{\dfrac{3d}{4}} &,& C_y = \dfrac{K\varepsilon_0 A}{\dfrac{d}{4}}
\end{matrix}Conforme associação em série:\begin{matrix}
C_1 = \dfrac{C_x \cdot C_y}{C_x + C_y} &\therefore& C_1 = \dfrac{4K\varepsilon_0 A}{d(3K+1)}
\end{matrix}Portanto, a razão solicitada é:\begin{matrix}
\dfrac{C_0}{C_1} = \dfrac{3K + 1}{4K}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}

