Existem diversas formas de analisar o problema, vamos começar pensando numa visão superior para uma análise mais qualitativa. Esboçando um circuito em que seu centro representa o extremo dos polos: 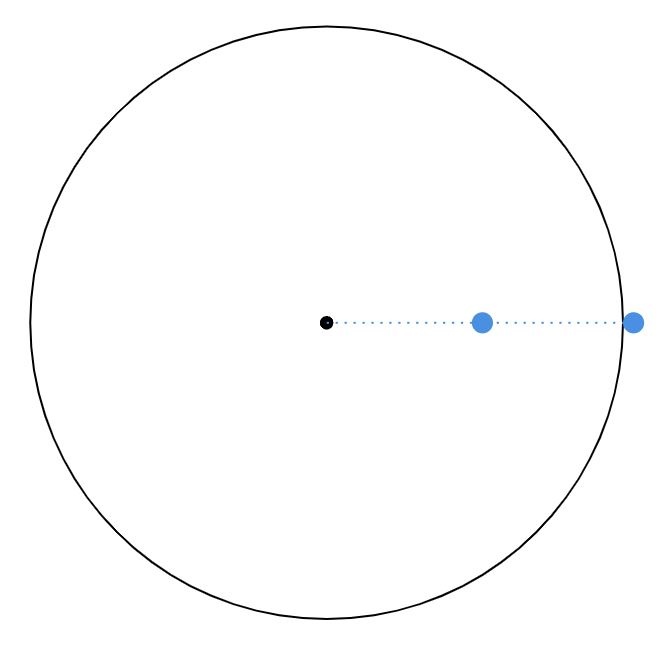Observe que o corpo na extremidade do círculo representa a latitude do equador, enquanto conforme o corpo se aproxima do centro, sua latitude aumenta. No caso, a ideia é perceber que conforme o corpo se aproxima do centro o raio de curvatura diminui, consequentemente, a força centrífuga que atua no corpo decresce, isto é, o peso aparente - aquele responsável pela leitura da balança - aumenta, visto que a força centrífuga tende a expelir o corpo. Nesse contexto, nota-se que o maior peso aparente será quando não houver força centrífuga, logo, o corpo deve se encontrar no centro, que representa a $\text{latitude de 90º}$, os polos da terra. Outra análise - mais quantitativa - seria pela vista lateral, a qual podemos esboçar de forma análoga: 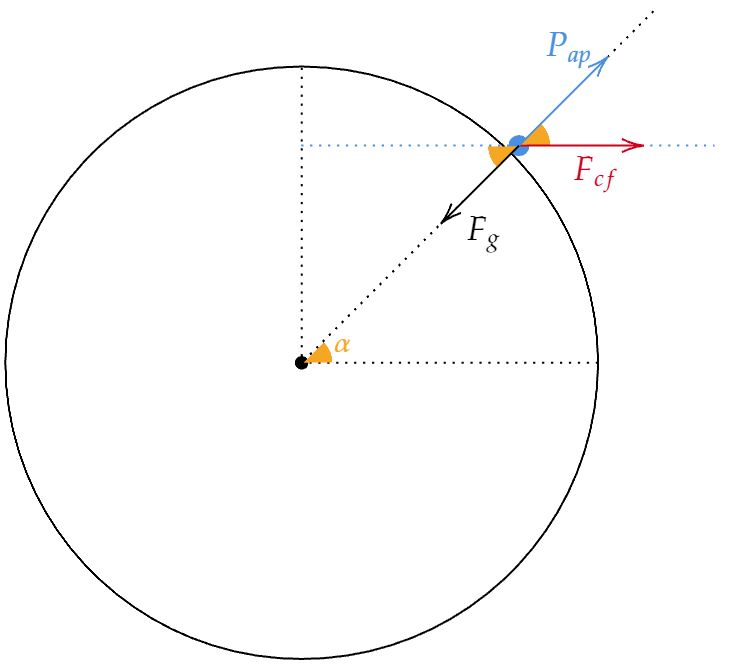Repare que o ângulo $\alpha$ é a latitude em questão, assim como $F_g$ a força gravitacional, $P_{ap}$ o peso aparente, e $F_{cf}$ a força centrífuga. Com isso, a análise se resume em decompor as forças e analisar o resultado:\begin{matrix} P_{ap} = F_g - \dfrac{F_{cf}}{\cos{\alpha}} \end{matrix}A situação é análoga, visando aumentar o peso aparente, a força centrípeta deve deixar de existir, isto é, $\alpha = 90º$.\begin{matrix}Letra \ (C) \end{matrix}