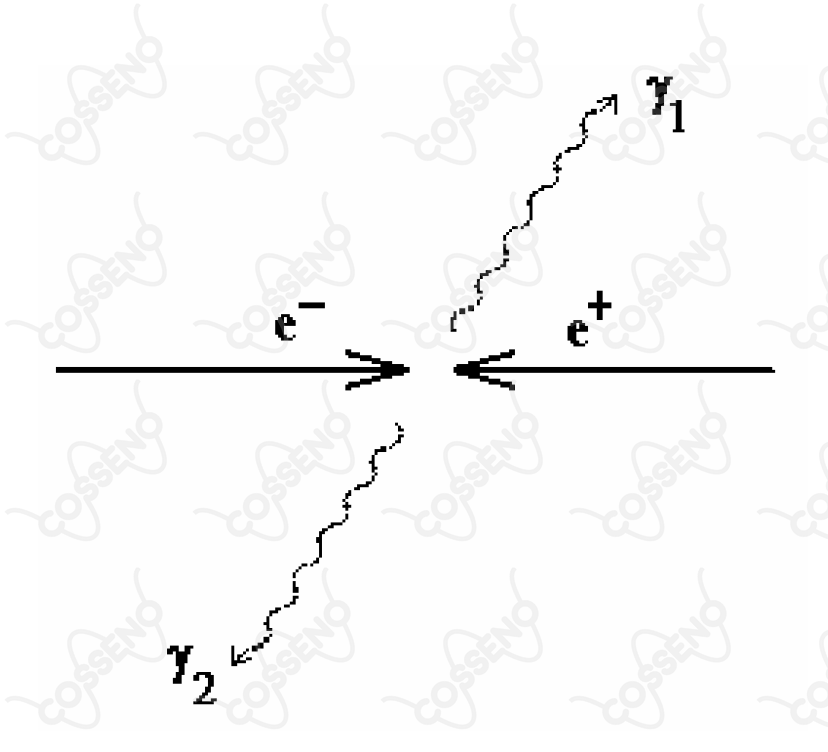
Um elétron e um pósitron, de massa , cada qual com energia cinética de e mesma quantidade de movimento, colidem entre si em sentidos opostos. Neste processo colisional as partículas aniquilam-se, produzindo dois fótons e . Indique os respectivos valores de energia e do comprimento de onda dos fótons.
Constante de Planck $h = 6,63 \times 10^{-34}\ J\cdot s$
Velocidade da luz $c = 3,00 \times 10^8\ m/s$
$1\ eV = 1{,}6 \times 10^{-19}\ J$
$1\text{ femtometro} = 1\ fm = 1 \times 10^{-15}\ m$
Velocidade da luz $c = 3,00 \times 10^8\ m/s$
$1\ eV = 1{,}6 \times 10^{-19}\ J$
$1\text{ femtometro} = 1\ fm = 1 \times 10^{-15}\ m$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pensando na energia dos corpos antes da colisão, podemos dividir ela em energia cinética e energia de repouso. Nesse contexto, pensando na conservação da energia, ao final da colisão o corpo desintegrado deve apresentar apenas a energia de um fóton, ou seja:\begin{matrix}
E_{inicial} = E_{final}
\end{matrix}\begin{matrix}
mc^2 + 1,20 = E
\end{matrix}Calculando $mc^2$ e convertendo para $\pu{MeV}$:\begin{matrix}
mc^2 = (9,11\times 10^{-31})(3,00\times 10^8)^2 \ \pu{J}
\end{matrix}\begin{matrix}
mc^2 = 81,99 \cdot 10^{14} \ \pu{J} \cdot \dfrac{1\pu{eV}}{1,6 \cdot 10^{-19} \ \pu{J}}
\end{matrix}\begin{matrix}
mc^2 = 0,512 \ \pu{MeV}
\end{matrix}Com isso, para a energia do fóton:\begin{matrix}
E = 0,512 + 1,20 \\ \boxed{E = 1,71 \ \pu{MeV}}
\end{matrix}Já para o comprimento de onda, pode-se partir da equação de Planck:\begin{matrix}
E = hf &\Rightarrow& E = h \dfrac{c}{\lambda} &\therefore& \lambda = \dfrac{hc}{E}
\end{matrix}Substituindo os devidos valores:\begin{matrix}
\lambda = \dfrac{(6,63\times 10^{-34})(3\times 10^8)}{(1,71\cdot 10^6)( 1,6 \cdot 10^{-19})} \\ \\
\lambda = 726 \cdot 10^{-15} \ \pu{m} \\
\boxed{\lambda = 726 \ \pu{fm}}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}$\color{orangered}{\text{Obs:}}$ Para encontrar $\lambda$ convertemos a energia do fóton de $\ce{MeV}$ para $\pu{J}$.

