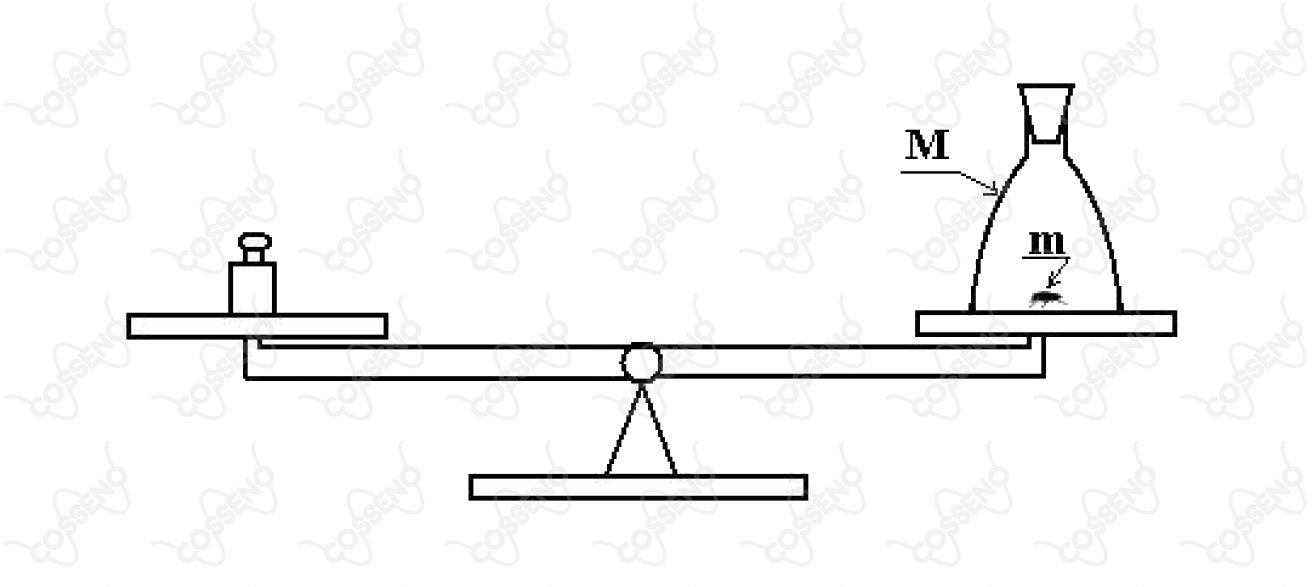
Num dos pratos de uma balança que se encontra em equilibrio estático, uma mosca de massa está em repouso no fundo de um frasco de massa . Mostrar em que condições a mosca poderá voar dentro do frasco sem que o equilíbrio seja afetado.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A balança está em equilíbrio quando o torque do peso da esquerda se iguala ao torque do peso da direita.
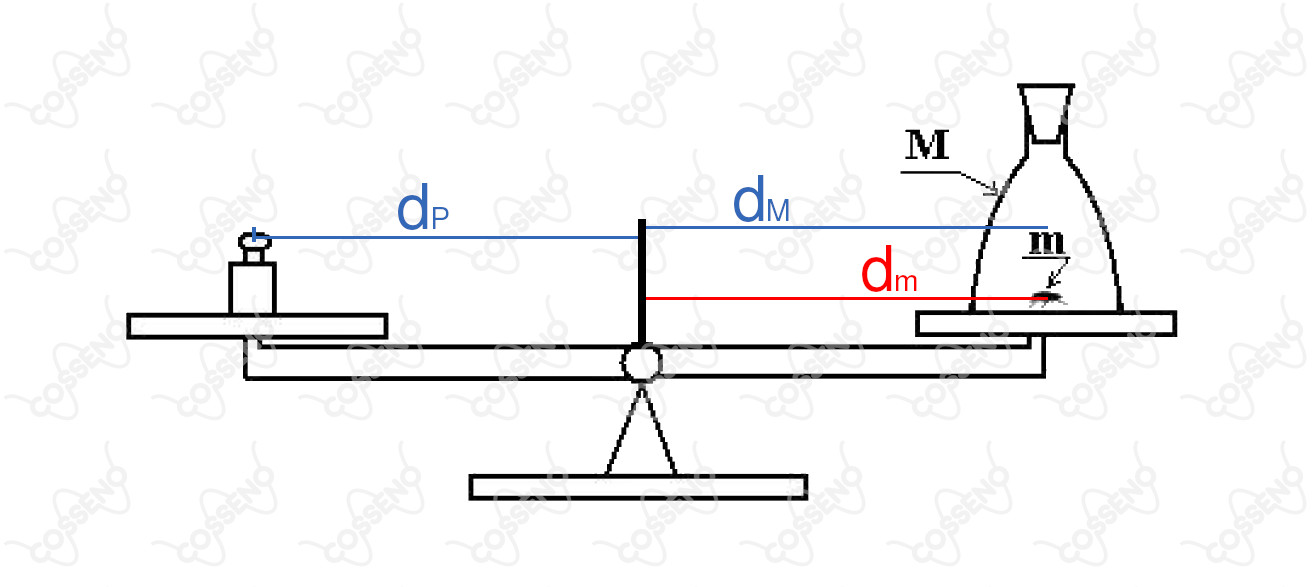 Assim: $$P\cdot d_P = Mg\cdot d_M + mg\cdot d_m$$
No entanto, para que a mosca levante voo do fundo do frasco até uma dada altura, ela deve imprimir uma força para baixo nas partículas gás. Isso faz com que ela garanta aceleração para cima, mas altera o equilíbrio rotacional do sistema: $$Mg\cdot d_M + mg\cdot d_m + \mathbf{F_{voo}} - P\cdot d_P > 0$$
Agora, caso a mosca já esteja em voo e em equilíbrio, basta que ela mantenha velocidade vertical constante (força resultante vertical nula) que o equilíbrio será mantido.
Portanto, basta que a mosca não tenha aceleração vertical para que o equilíbrio não se altere.
---
Agora, o que a grande maioria das resoluções na internet não comenta é que ainda há uma segunda possibilidade.
É possível que a mosca execute um movimento que mantém a soma $mg\cdot d_m + \mathbf{F_\text{voo}}$ constante, bastando que as taxas de diminuição da distância $d$ e aumento da força $\mathbf{F_\text{voo}}$ obedeçam à equação: $$mg\cdot \dfrac{\Delta d_m}{\Delta t} + \dfrac{\Delta \mathbf{F_\text{voo}}}{\Delta t} = 0$$
Assim: $$P\cdot d_P = Mg\cdot d_M + mg\cdot d_m$$
No entanto, para que a mosca levante voo do fundo do frasco até uma dada altura, ela deve imprimir uma força para baixo nas partículas gás. Isso faz com que ela garanta aceleração para cima, mas altera o equilíbrio rotacional do sistema: $$Mg\cdot d_M + mg\cdot d_m + \mathbf{F_{voo}} - P\cdot d_P > 0$$
Agora, caso a mosca já esteja em voo e em equilíbrio, basta que ela mantenha velocidade vertical constante (força resultante vertical nula) que o equilíbrio será mantido.
Portanto, basta que a mosca não tenha aceleração vertical para que o equilíbrio não se altere.
---
Agora, o que a grande maioria das resoluções na internet não comenta é que ainda há uma segunda possibilidade.
É possível que a mosca execute um movimento que mantém a soma $mg\cdot d_m + \mathbf{F_\text{voo}}$ constante, bastando que as taxas de diminuição da distância $d$ e aumento da força $\mathbf{F_\text{voo}}$ obedeçam à equação: $$mg\cdot \dfrac{\Delta d_m}{\Delta t} + \dfrac{\Delta \mathbf{F_\text{voo}}}{\Delta t} = 0$$

Ampliar Imagem

