A figura mostra uma barra de de comprimento e massa desprezível, suspensa por uma corda , sustentando um peso de no ponto indicado. Sabendo que a barra se apóia sem atrito nas paredes do vão, a razão entre a tensão na corda e a reação na parede no ponto , no equilíbrio estático, é igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 
A princípio, vamos colocar as forças que atuam na barra:
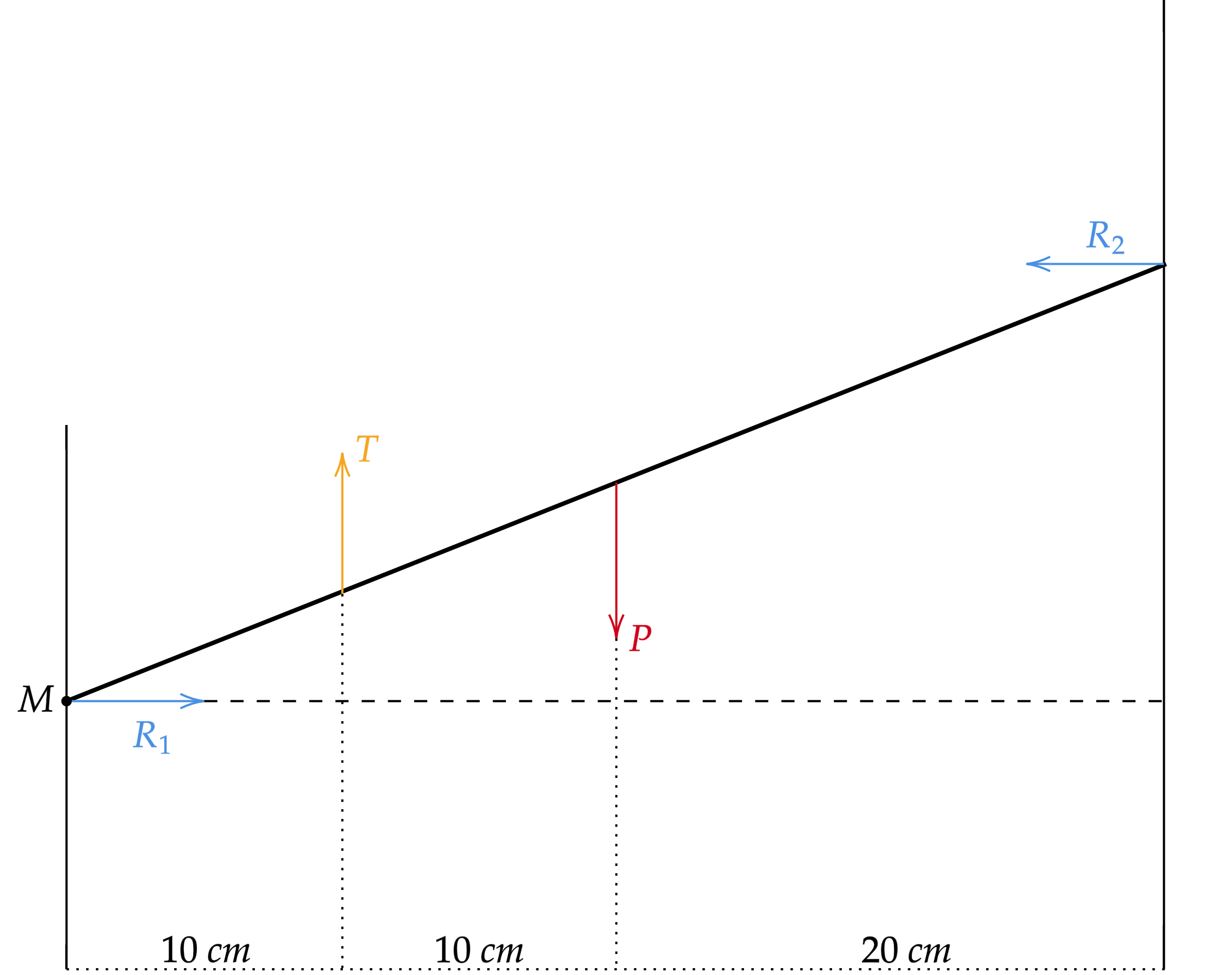Como o equilíbrio é estático, vamos partir do equilíbrio das forças:\begin{matrix} \text{Vertical:} & P = T \\ \text{Horizontal:} & R_1 = R_2
\end{matrix}Agora, analisando o momento das forças em relação ao ponto $M$ da imagem: \begin{matrix} R_2 \cdot d + T \cdot 10 = P \cdot 20
\end{matrix}Observe que $d$ pode ser facilmente encontrado aplicando o $\text{teorema de Pitágoras}$:\begin{matrix}
50^2 = 40^2 + d^2 \\
d = 30 \ \pu{cm}
\end{matrix}Com isso,\begin{matrix}
R_2 \cdot 30 + T \cdot 10 = P \cdot 20 \\
3R_2 + T = 2T \\ \boxed{\dfrac{T}{R_2} =3,0} \\ \\ Letra \ (B)
\end{matrix}
Ampliar Imagem
