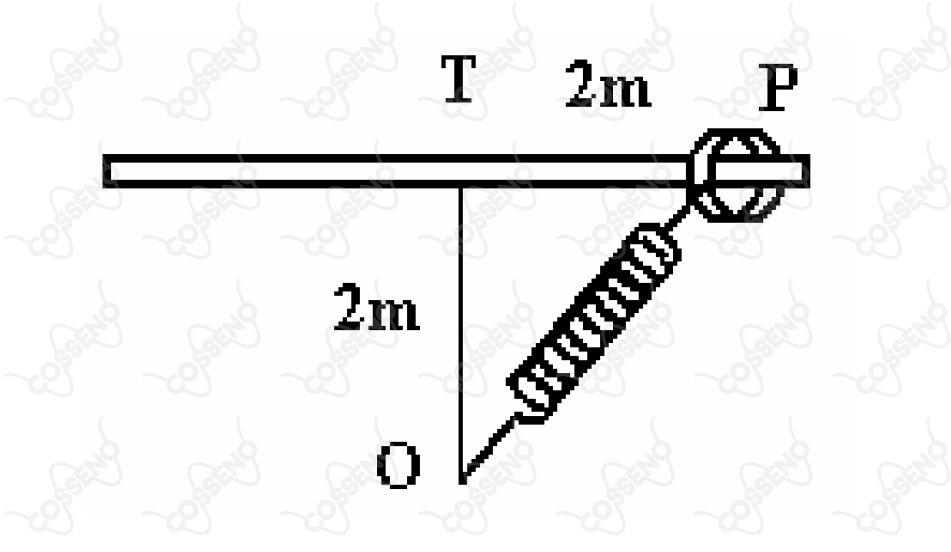
Um aro de de massa encontra-se preso a uma mola de massa desprezível, constante elástica e comprimento inicial quando não distendida, afixada no ponto . A figura mostra o aro numa posição em uma barra horizontal fixa ao longo da qual o aro pode deslizar sem atrito. Soltando o aro do ponto , qual deve ser sua velocidade, em , ao alcançar o ponto , a de distância?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Admitindo que não haja forças dissipativas, a questão se resume numa conservação da energia mecânica. Inicialmente, toda energia do anel é potencial elástica, assim quando ele passa por $T$ sua energia potencial elástica decresce se convertendo em cinética. Com isso, pode-se escrever:\begin{matrix}
\dfrac{k(\overline{OP} - L_0)^2}{2} = \dfrac{k(\overline{OT} - L_0)^2}{2} + \dfrac{mv^2}{2}
\end{matrix}Observe que encontrar $\overline{OP}$ não é difícil, basta aplicar o teorema de Pitágoras:\begin{matrix}
(\overline{OP})^2 = (\overline{OT})^2 + (\overline{TP})^2
\end{matrix}\begin{matrix}
\overline{OP} = 2\sqrt{2}
\end{matrix}Substituindo os dados e resultados encontrados na primeira expressão:\begin{matrix}
\dfrac{10(2\sqrt{2} - 1)^2}{2} = \dfrac{10(2 - 1)^2}{2} + \dfrac{v^2}{2}
\end{matrix}\begin{matrix}
v^2 = 10(8 - 4\sqrt{2})
\end{matrix}\begin{matrix}v = \sqrt{40(2 - \sqrt{2})}
\end{matrix}$\color{orangered}{\text{Obs:}}$ $\sqrt{2} \approx 1,415$\begin{matrix}
\boxed{v \approx \sqrt{23,4}} \\ \\ Letra \ (C)
\end{matrix}

