Sejam subconjuntos de tais que , , , . Então o conjunto é igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, é possível esboçar os Diagramas de Euler-Venn com os quatro conjuntos e ir ponderando os resultados do enunciado. Contudo, podemos fazer algo utilizando as propriedades dos conjuntos, isso conferindo com os Diagramas de Euler-Venn caso necessário. (Basicamente, iremos tentar driblar os quatro conjuntos a fim de agilizar o raciocínio, pode ser um pouco difícil visualizar tudo com quatro conjuntos.) Comecemos pelas primeiras informações do enunciado, são elas:\begin{matrix}
(X -Y) \cap Z &,& Z \cap Y = \emptyset
\end{matrix}Observe que os conjuntos $Z$ e $Y$ são disjuntos. (Isso poderia lhe ajudar a esboçar os quatro conjuntos.) Dessa forma, podemos fazer:\begin{matrix}
(X -Y) \cap Z = (X \cap Z) - (Y\cap Z) = (X \cap Z) - \emptyset \\
(X \cap Z) = \{ 1,2,3,4 \}
\end{matrix}$\color{orangered}{\text{Obs:}}$ Caso tenha dificuldade de interpretar o resultado acima (assim como os demais), tente desenhar os conjuntos e verificar a veracidade da propriedade. Vale ressaltar que a ideia é justamente essa: reduzir o raciocínio fazendo a análise em partes - com menos de quatro conjuntos.
Continuando, temos:\begin{matrix}
W \cap (X -Z) = (W \cap X) - (W \cap Z) = (W \cap X) - (X \cap Z) \end{matrix}
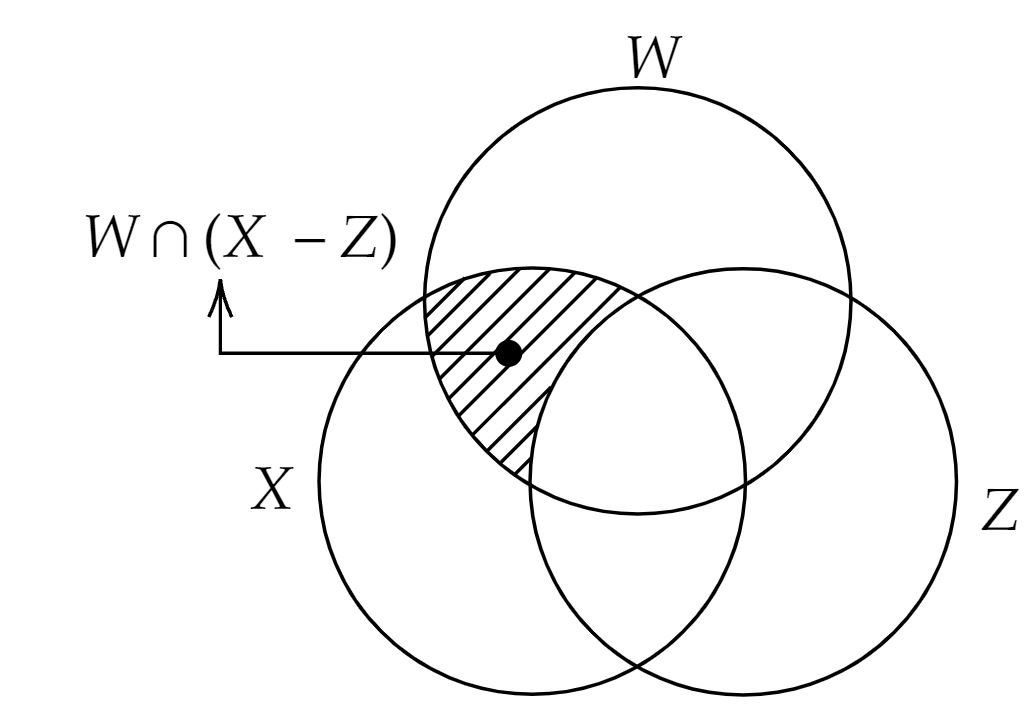 \begin{matrix}
(W \cap X) - (X \cap Z) = \{7,8\}
\end{matrix}
\begin{matrix}
(W \cap X) - (X \cap Z) = \{7,8\}
\end{matrix}
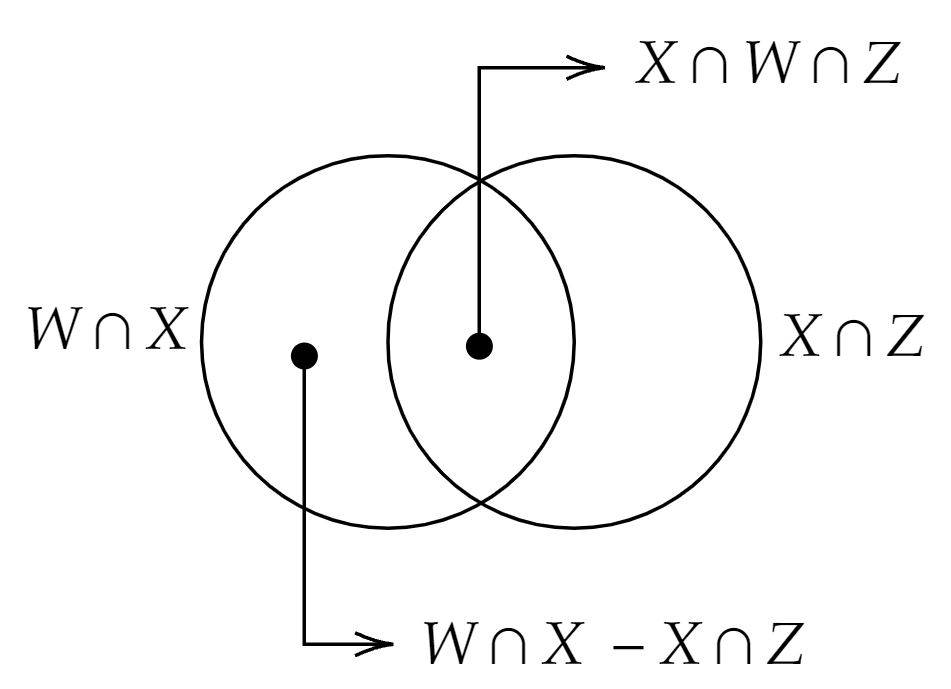 Pensando nos conjuntos solicitados:\begin{matrix}
X \cap (Z \cup W) = (X \cap Z) \cup (X \cap W) \\ \\
X \cap (Z \cup W) = \{ 1,2,3,4,7,8\}
\end{matrix}Subtraindo a outra parte:\begin{matrix} X \cap (Z \cup W) - W \cap (Y \cup Z) \\ \color{gray}{A -B = A - A\cap B}\\
X \cap (Z \cup W) - [X \cap (Z \cup W) ] \cap [W \cap (Y \cup Z) ] \end{matrix}Repare que $Y$ é irrelevante no resultado acima, visto que em $(Y \cup Z)$ iremos filtrar $Z$, assim como em $(Z \cup W)$ estaremos filtrando $Z$ e $W$. No caso, a ideia aqui é perceber que como $Z \cap Y$ é vazio, não há valor a ser computado, resultando em: \begin{matrix}
X \cap (Z \cup W) - X\cap W \cap Z
\end{matrix}Portanto,\begin{matrix}\boxed{
X \cap (Z \cup W) - W \cap (Y \cup Z) = \{1,3,7,8\}}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}
Pensando nos conjuntos solicitados:\begin{matrix}
X \cap (Z \cup W) = (X \cap Z) \cup (X \cap W) \\ \\
X \cap (Z \cup W) = \{ 1,2,3,4,7,8\}
\end{matrix}Subtraindo a outra parte:\begin{matrix} X \cap (Z \cup W) - W \cap (Y \cup Z) \\ \color{gray}{A -B = A - A\cap B}\\
X \cap (Z \cup W) - [X \cap (Z \cup W) ] \cap [W \cap (Y \cup Z) ] \end{matrix}Repare que $Y$ é irrelevante no resultado acima, visto que em $(Y \cup Z)$ iremos filtrar $Z$, assim como em $(Z \cup W)$ estaremos filtrando $Z$ e $W$. No caso, a ideia aqui é perceber que como $Z \cap Y$ é vazio, não há valor a ser computado, resultando em: \begin{matrix}
X \cap (Z \cup W) - X\cap W \cap Z
\end{matrix}Portanto,\begin{matrix}\boxed{
X \cap (Z \cup W) - W \cap (Y \cup Z) = \{1,3,7,8\}}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}

Ampliar Imagem
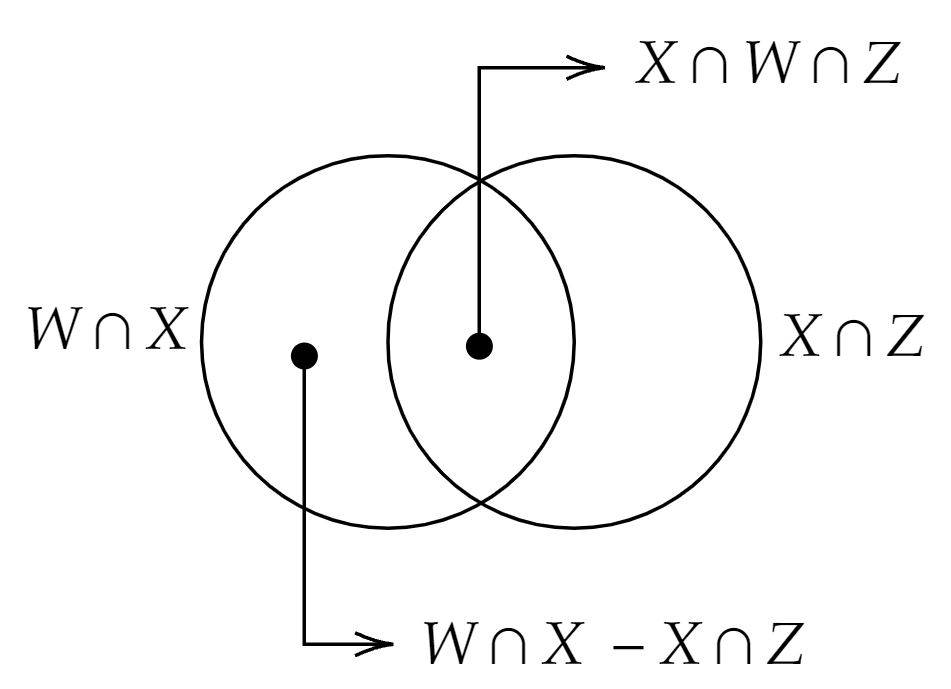
Ampliar Imagem

