Imaginando a situação, podemos esboçar algo como: 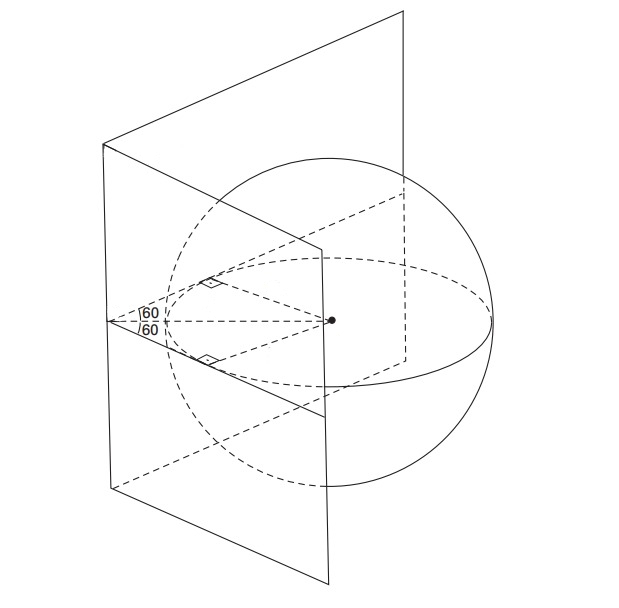Note que podemos planificar a situação por uma visão superior, o que ficará como: 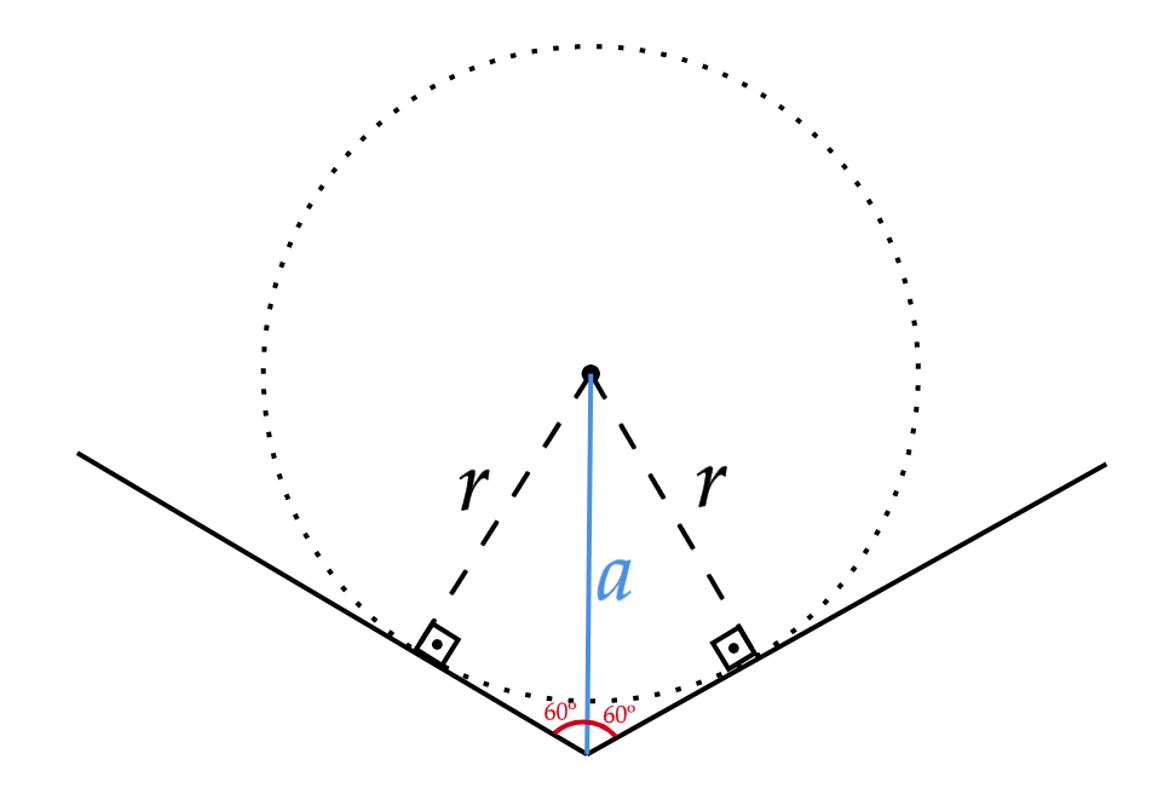Agora, o problema já está quase resolvido, resta fazer:\begin{matrix} \sin{60º} = \dfrac{r}{a} &\Rightarrow& \dfrac{r}{a} = \dfrac{\sqrt{3}}{2} &\Rightarrow& a = \dfrac{2}{\sqrt{3}}r \end{matrix}Conforme volume da esfera, podemos encontrar $r$:\begin{matrix} \dfrac{4}{3}\pi r^3 = 4\sqrt{3}\pi &\therefore& r = \sqrt{3} \ \pu{cm} \end{matrix}Concluímos então que:\begin{matrix}\boxed{a = 2 \ \pu{cm}} \end{matrix}\begin{matrix}Letra \ (E) \end{matrix}