Esboçando a situação: 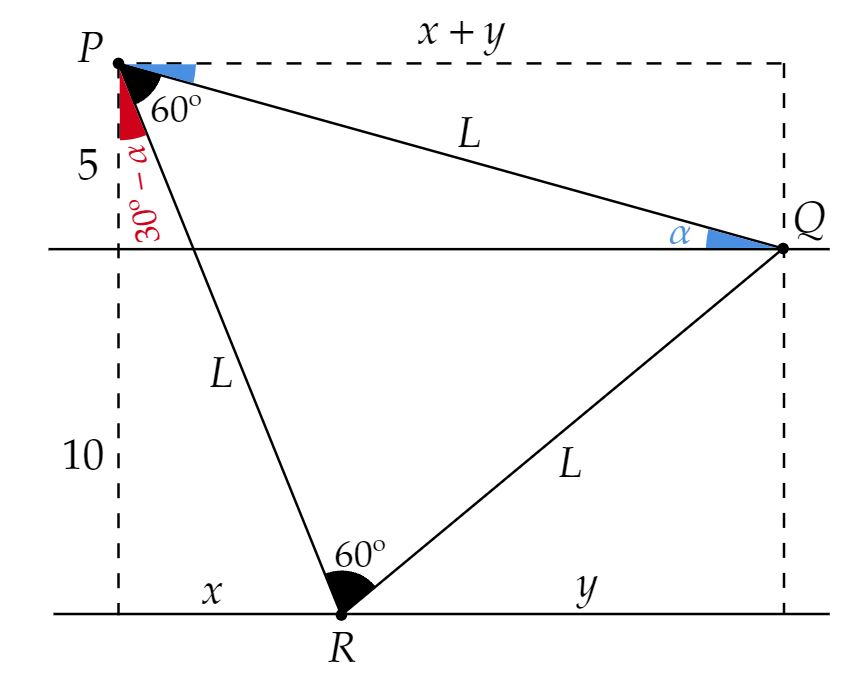Veja que existem diversas formas de resolver esta questão, então deixarei duas, são elas: $• \ \text{Resolução I:}$ Observe que temos três triângulos retângulos sendo suas hipotenusas igual ao lado do triângulo equilátero. Com isso, pode-se escrever:\begin{matrix} (1): & L^2 &=& (x+y)^2 &+& 5^2 \\ (2): & L^2 &=& x^2 &+& 15^2 \\ (3): & L^2 &=& y^2 &+& 10^2 \end{matrix}Por $(2)$ e $(3)$, têm-se respectivamente:\begin{matrix}x = \sqrt{L^2 - 15^2 } &,& y = \sqrt{L^2 - 10^2} \end{matrix}Substituindo os resultado acima em $(1)$:\begin{matrix} L^2 = ( \sqrt{L^2 - 15^2 } +\sqrt{L^2 - 10^2} )^2 + 5^2 \end{matrix}\begin{matrix}3L^4 - 700L^2 = 0 \end{matrix}\begin{matrix}L^2 (3L^2 - 700) = 0 \end{matrix}É evidente que $L^2 = 0$ é inviável, logo:\begin{matrix} 3L^2 - 700 = 0 &\therefore& L = \sqrt{\dfrac{700}{3}} \end{matrix}Como o triângulo é equilátero, sua área e seu perímetro são, respectivamente:\begin{matrix} [PQR] &=& \dfrac{L^2\sqrt{3}}{4} &=& 175 \dfrac{\sqrt{3}}{3} & \tiny{\blacksquare} \\ \\ 2p &=& 3L &=& 10\sqrt{21} & \tiny{\blacksquare} \end{matrix} $• \ \text{Resolução II:}$ Por trigonometria, é possível fazer:\begin{matrix} \cos{(30º - \alpha)} = \cos{30º}\cos{\alpha} + \sin{30º}\sin{\alpha} \end{matrix}\begin{matrix} \dfrac{15}{L} = \dfrac{\sqrt{3}}{2} \left( \dfrac{x+y}{L} \right) + \dfrac{1}{2} \left( \dfrac{5}{L} \right) \end{matrix}\begin{matrix}(x+y) =\dfrac{25\sqrt{3}}{3} \end{matrix}Substituindo o resultado acima em $(1)$ da resolução anterior:\begin{matrix} L^2 = \left( \dfrac{25\sqrt{3}}{3} \right)^2 + 5^2 &\therefore& L = \sqrt{\dfrac{700}{3}} \end{matrix}A partir daqui o raciocínio é análogo ao anterior.\begin{matrix}Letra \ (B) \end{matrix}