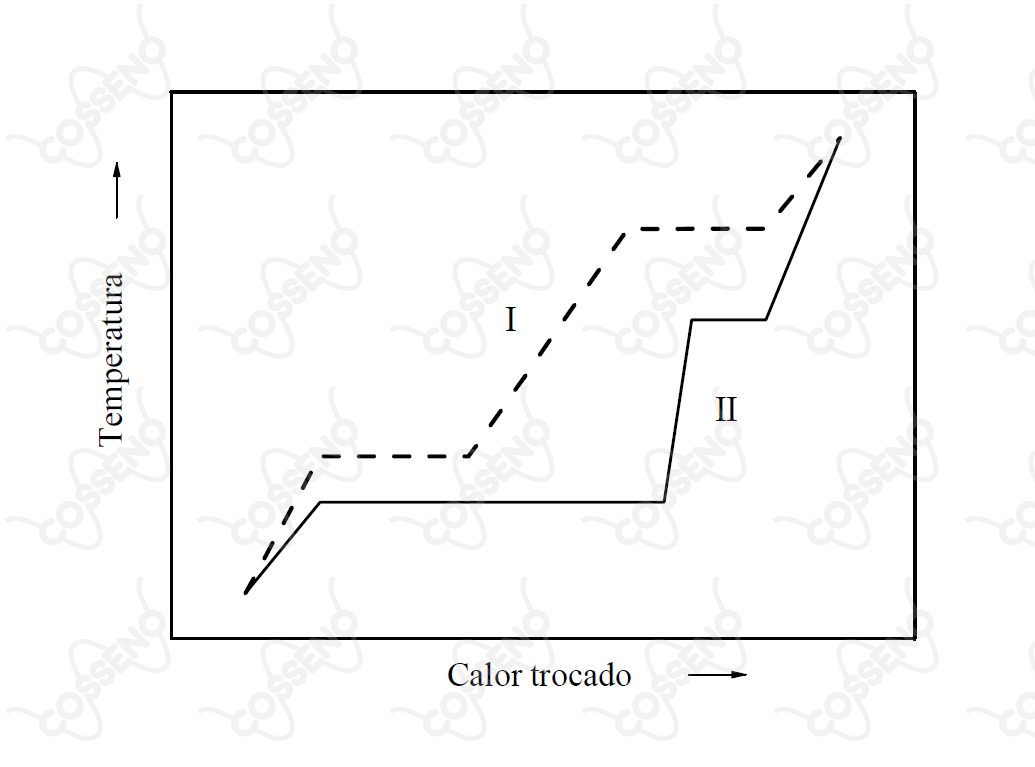
Amostras de massas iguais de duas substâncias, I e II, foram submetidas independentemente a um processo de aquecimento em atmosfera inerte e a pressão constante. O gráfico abaixo mostra a variação da temperatura em função do calor trocado entre cada uma das amostras e a vizinhança.
Assinale a opção ERRADA em relação à comparação das grandezas termodinâmicas.
Dados:
$\Delta H_f$ e $\Delta H_v$ representam as variações de entalpia de fusão e de vaporização$,$ respectivamente$,$ e $c_p$ é o calor específico.
$\Delta H_f$ e $\Delta H_v$ representam as variações de entalpia de fusão e de vaporização$,$ respectivamente$,$ e $c_p$ é o calor específico.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Alternativa (A):}$ $\color{#3368b8}{\text{Correta}}$
Com conhecimento que a entalpia é uma função de estado, necessitamos apenas avaliar os pontos de início e fim da fusão, isto é, avaliar quem variou mais o calor trocado durante o processo. Nesse sentido, observe o gráfico, ambas as substâncias começam a fundir num calor muito próximo, contudo, ao seguir suas respectivas linhas de fusão, a substância $\text{II}$ vai muito adiante, demonstrando maior necessidade de calor, ou seja:\begin{matrix}\Delta H_f(I) < \Delta H_f(II)
\end{matrix}$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Incorreta}}$
Num raciocínio análogo ao anterior, nota-se que para vaporização o resultado é o contrário, ambas terminam numa entalpia muito próxima, e iniciam em entalpias diferentes. Novamente, analisando as linhas, nota-se:\begin{matrix}\Delta H_v(I) > \Delta H_v(II)
\end{matrix}$• \ \text{Alternativa (C, D e E):}$ $\color{#3368b8}{\text{Corretas}}$
A ideia consiste em perceber que o calor específico é, grosseiramente: \begin{matrix}c_p = \dfrac{\Delta \text{(Calor trocado)}}{\Delta \text{(Temperatura)}}
\end{matrix}O que equivale a cotangente da inclinação das retas, analisando o gráfico - mais precisamente as inclinações - todos os resultados seguem corretos.\begin{matrix}Letra \ (B)
\end{matrix}

