O processo é análogo à osmose, pense em duas câmaras hermeticamente fechadas, em uma colocamos o frasco com $X$, já na outra o fraco com $Y$. Nesse sentido, nós iremos conectar os dois sistemas, estes irão interagir a partir do conceito de $\text{tendência ao escape}$, mais precisamente, as taxas de condensação e vaporação dos líquidos. Com isso, deve-se ter conhecimento sobre propriedades coligativas, ao menos o suficiente para entender que quanto maior a quantidade de soluto não volátil (sal nesse caso) menor é a tendência ao escape das moléculas do líquido. Nós podemos justificar isso pelo fato que ao haver soluto não volátil, partículas diferentes que precisam de mais energia para escapar irão tomar lugares de partículas do líquido na superfície, ou seja, o processo de evaporação será diminuído, pois o que antes saia agora não sai. Desse modo, já podemos dizer que a taxa de evaporação de $Y$ é maior que a de $X$, visto que ela está mais diluída, isto é, menos soluto atrapalha o processo de evaporação. Analogamente, precisamos pensar agora na taxa de condensação, qual será o comportamento dela? Talvez seja um pouco tácito, mas ela será a mesma para os dois líquidos. No caso, a taxa de condensação varia conforme alguns (vários dependendo do caso) parâmetros, mas o ponto aqui não é esse, e sim que a taxa de condensação não faz parte de dois sistemas $X$ e $Y$, mas um que compõe $X$ e $Y$. Nesse ponto, a ideia é perceber que para taxas de condensação diferentes, precisaríamos de zonas diferentes no sistema, isto é, regiões em que a temperatura, pressão, e entre outros parâmetros fossem distintos dos demais. Contudo, não há isso, o sistema todo adquire uma determinada pressão, uma determinada temperatura e assim vai, logo, não há nada que permita uma região condensar mais que outra - estamos obviamente admitindo o idealismo. Em suma, podemos listar dois resultados:\begin{matrix} (1): & \text{A taxa de evaporação de $Y$ é maior que a de $X$}\\ (2): & \text{As taxas de condensação são idênticas} \end{matrix}Pode-se esboçar a situação como: 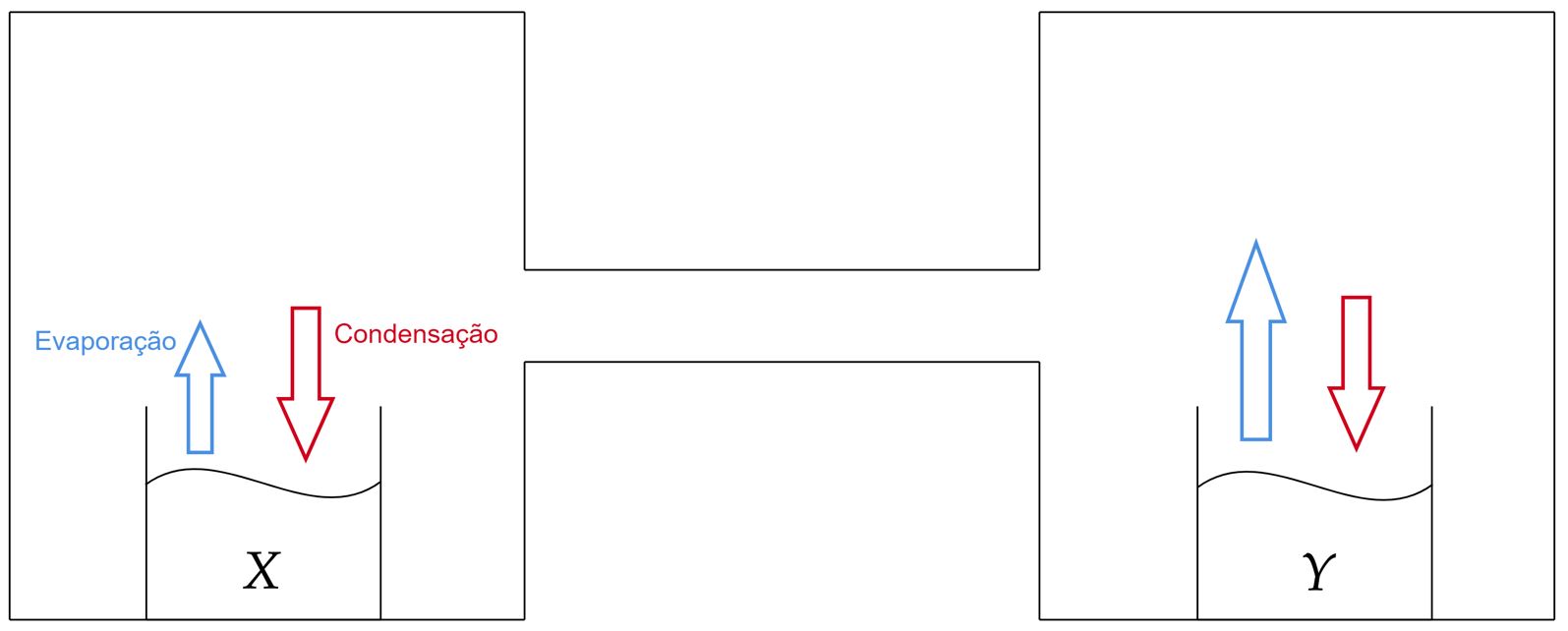Agora, o problema já está resolvido, pois basta perceber que com $Y$ evaporando mais que $X$ e condensando menos, tem-se que o volume de $Y$ irá diminuir, assim como o de $X$ irá aumentar, visto que ele irá condensar mais solvente do que realmente evapora. Por outro lado, pensando na solução $Y$, esta deverá estar mais concentrada ao final do processo, visto que seu solvente irá evaporar, reduzindo o volume da solução, consequentemente, aumentando a concentração. Dessa forma, a pressão de vapor inicial em $Y$ era maior, visto que estava mais diluída. Portanto, constata-se:\begin{matrix}VX_i < VX_f &,& PY_i > P_f \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}$\color{orangered}{\text{Obs:}}$ Após certo tempo o sistema irá entrar em equilíbrio dinâmico, as taxas de condensação e evaporação serão as mesmas. Todavia, conforme a osmose, um irá transferir solvente para o outro ao ponto que as concentrações sejam as mesmas - condição necessária neste caso para que as taxas sejam as mesmas. Além disso, você poderia tentar avaliar o problema quantitativamente pelas $\text{leis de Raoult e Henry}$, estas que apenas traduziriam o trabalho qualitativo que fizemos.