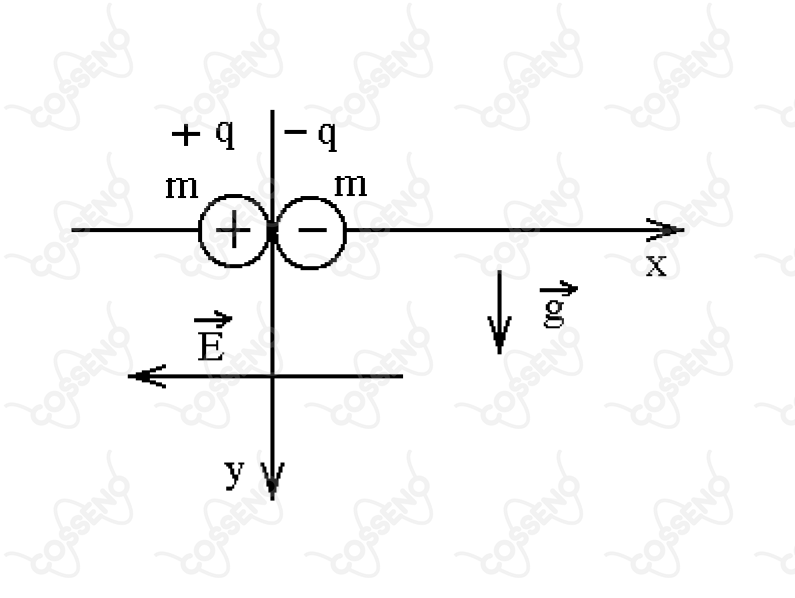
Duas cargas pontuais e , de massas iguais , encontram-se inicialmente na origem de um sistema cartesiano e caem devido ao próprio peso a partir do repouso, bem como devido à ação de um campo elétrico horizontal e uniforme , conforme mostra a figura.
Por simplicidade, despreze a força coulombiana atrativa entre as cargas e determine o trabalho realizado pela força peso sobre as cargas ao se encontrarem separadas entre si por uma distância horizontal .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Resolução I: Cinemática} $
A priori, não é difícil perceber que temos movimento acelerado nos dois eixos, no eixo $x$ divido a força elétrica, já no eixo $y$ por conta da força peso. Dessa forma, podemos escrever o trabalho da força peso de uma das cargas como:
\begin{matrix} W_P = mg\Delta y
\end{matrix}Atente que, as forças são idênticas em módulo, isto é, a trajetória de cada partícula será a mesma. Além disso, devemos expressar o trabalho em função das informações fornecidas no enunciado, assim, necessita-se encontrar um $\Delta y$ adequado. Com isso, podemos analisar cinematicamente uma partícula em cada eixo, comecemos pelo eixo $y$:\begin{matrix} \Delta y = v_{0y}t + g {\dfrac{\Delta t^2}{2}} &\Rightarrow & \Delta y = g {\dfrac{\Delta t^2}{2}}
\end{matrix}$\color{orangered}{Obs:}$ $ v_{0y} = 0$ , pois parte do repouso.
Agora, ao analisar o eixo $x$: \begin{matrix} \dfrac{d}{2} = v_{0x}t + a_x {\dfrac{\Delta t^2}{2}} &\Rightarrow & d = a_x \Delta t^2
\end{matrix}$\color{orangered}{Obs:}$ $ v_{0x} = 0$ , pois parte do repouso. Além de que, cada partícula move-se metade da distância que as separam.
• $a_x$: \begin{matrix} F_r = F_{ele} &\Rightarrow & m a_x = Eq &\Rightarrow & \fbox{$a_x = {\dfrac{Eq}{m}}$}
\end{matrix}Concluindo,\begin{matrix} \fbox{$\Delta t^2 = {\dfrac{dm}{Eq}}$}
\end{matrix}Com nossos resultados retirados da análise do eixo $x$, já podemos definir $\Delta y$ adequadamente. \begin{matrix} \fbox{$\Delta y = {\dfrac{mgd}{2Eq}}$}
\end{matrix}Substituindo $\Delta y$ na expressão do trabalho, e não esquecendo o fato de querermos todo o trabalho realizado pela força peso, isto é, $\text{ o trabalho da força peso realizado nas duas cargas}$, temos: \begin{matrix} W_T = 2W_P &\Rightarrow &\fbox{$W_T= {\dfrac{m^2g^2d}{Eq}}$}
\end{matrix}
$• \ \text{Resolução II: Semelhança}$
Uma outra saída para a questão seria analisar a resultante das forças em cada partícula, perceba que, a trajetória de ambas seria uma diagonal com sentido positivo ao eixo $y$ da imagem. Por conseguinte, pode-se perceber que em cada partícula, a distância horizontal percorrida $(\frac{d}{2})$, a distância vertical percorrida $(\Delta y)$, e a trajetória percorrida, formam um triângulo retângulo. Destarte, façamos uma semelhança entre o triângulo formado pelas trajetórias, e aquele formado pelos vetores das forças:\begin{matrix} {\dfrac{P}{F_{ele}} = \dfrac{\Delta y}{\dfrac{d}{2}}} &\Rightarrow & \fbox{$\Delta y = {\dfrac{mgd}{2Eq}}$}
\end{matrix}Portanto, segue análoga a ideia da resolução I.

