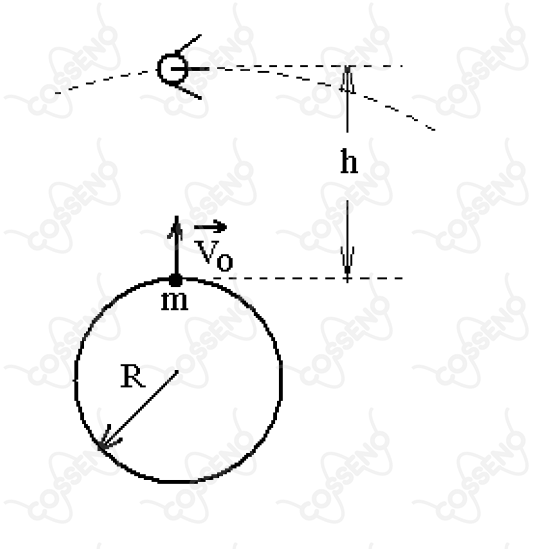
Lançado verticalmente da Terra com velocidade inicial , um parafuso de massa chega com velocidade nula na órbita de um satélite artificial, geoestacionário em relação à Terra, que se situa na mesma vertical. Desprezando a resistência do ar, determine a velocidade V0 em função da aceleração da gravidade na superfície da Terra, raio da Terra e altura do satélite.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Conservando Energia Mecânica na Terra e na altura $h$.
$$\dfrac{mv_{0}^{2}}{2} - \dfrac{GMm}{R} = - \dfrac{GMm}{R+h} \Rightarrow v_{0}^{2} = \dfrac{2GMh}{R(R+h)}.$$
Lembrando que $g = \dfrac{GM}{R^{2}},$ por $P = F_{g}.$
Com isso,
$$v_{0} = \sqrt{\dfrac{2ghR}{R+h}}.$$

