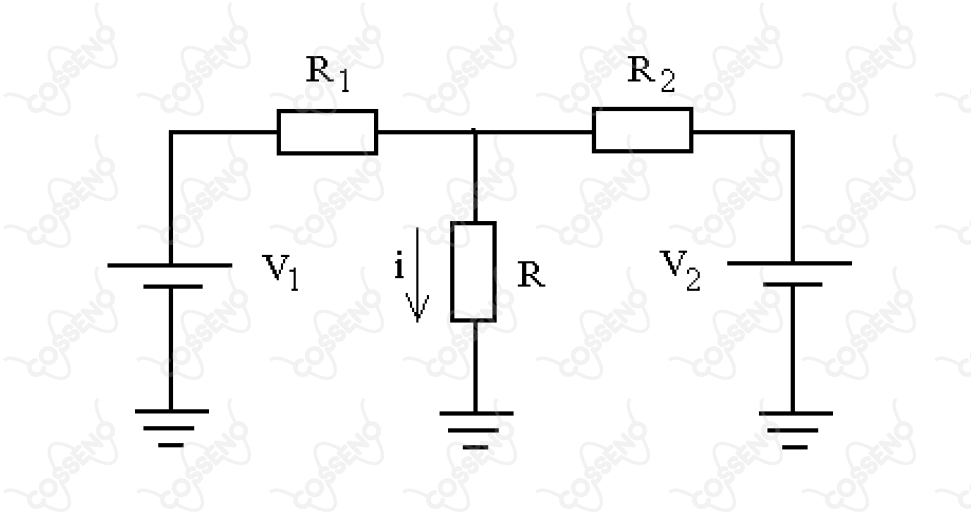
No circuito da figura, têm-se as resistências e as fontes e aterradas. A corrente indicada é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Como tudo está aterrado, podemos reescrever o circuito como:
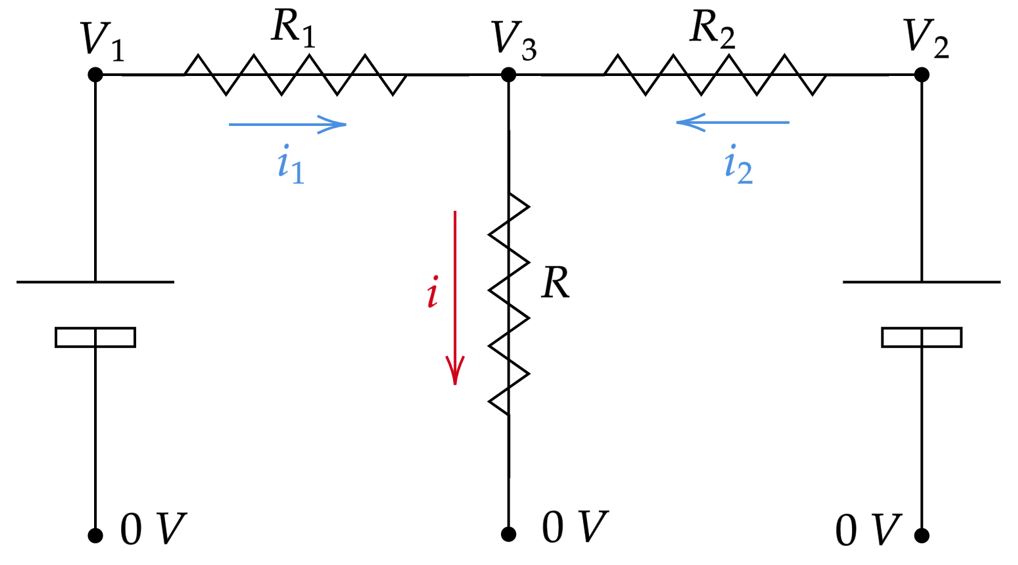 Pela $\text{Lei de Ohm Generalizada}$, têm-se: \begin{matrix} V_3 = Ri &,& V_1 - V_3 = R_1 i_1 &,& V_2 - V_3 = R_1 i_1 &,& i = i_1 + i_2
\end{matrix}Continuando, \begin{matrix} i_1 = \large{\frac{V_1 - V_3}{R_1}} &,& i_2 = {\dfrac{V_2 - V_3}{R_2}} &\Rightarrow& i = {{\dfrac{V_1 - V_3}{R_1}}} + {{\dfrac{V_2 - V_3}{R_2}}}
\end{matrix}Substituindo $V_3$: \begin{matrix} \fbox{$ i = {{\dfrac{(V_1R_2 + V_2R_1)}{(R_1R_2 + RR_2 + RR_1)}}} $} \\ \\ Letra \ (D)
\end{matrix}
Pela $\text{Lei de Ohm Generalizada}$, têm-se: \begin{matrix} V_3 = Ri &,& V_1 - V_3 = R_1 i_1 &,& V_2 - V_3 = R_1 i_1 &,& i = i_1 + i_2
\end{matrix}Continuando, \begin{matrix} i_1 = \large{\frac{V_1 - V_3}{R_1}} &,& i_2 = {\dfrac{V_2 - V_3}{R_2}} &\Rightarrow& i = {{\dfrac{V_1 - V_3}{R_1}}} + {{\dfrac{V_2 - V_3}{R_2}}}
\end{matrix}Substituindo $V_3$: \begin{matrix} \fbox{$ i = {{\dfrac{(V_1R_2 + V_2R_1)}{(R_1R_2 + RR_2 + RR_1)}}} $} \\ \\ Letra \ (D)
\end{matrix}

Ampliar Imagem
Ampliar Imagem


