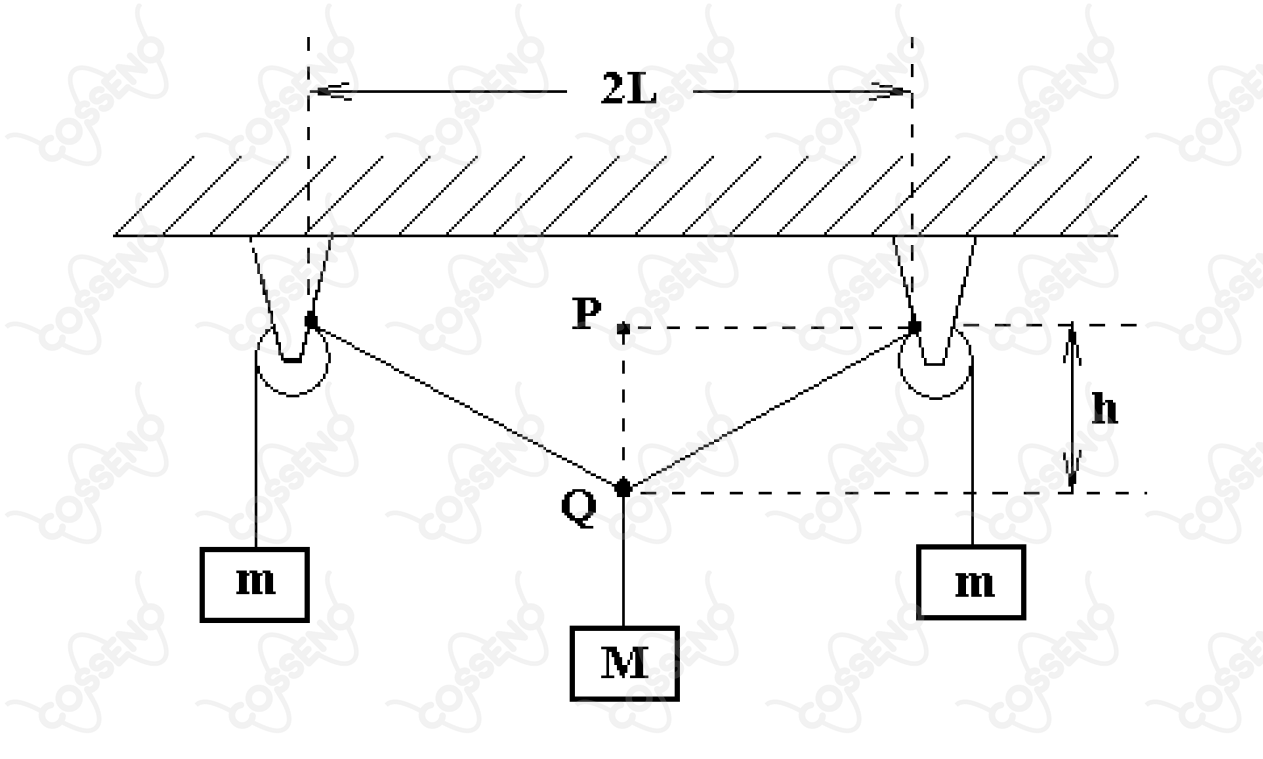
No arranjo mostrado na figura com duas polias, o fio inextensível e sem peso sustenta a massa e, também, simetricamente, as duas massas , em equilíbrio estático. Desprezando o atrito de qualquer natureza, o valor da distância entre os pontos e vale
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Adicionando as forças aos elementos do sistema:
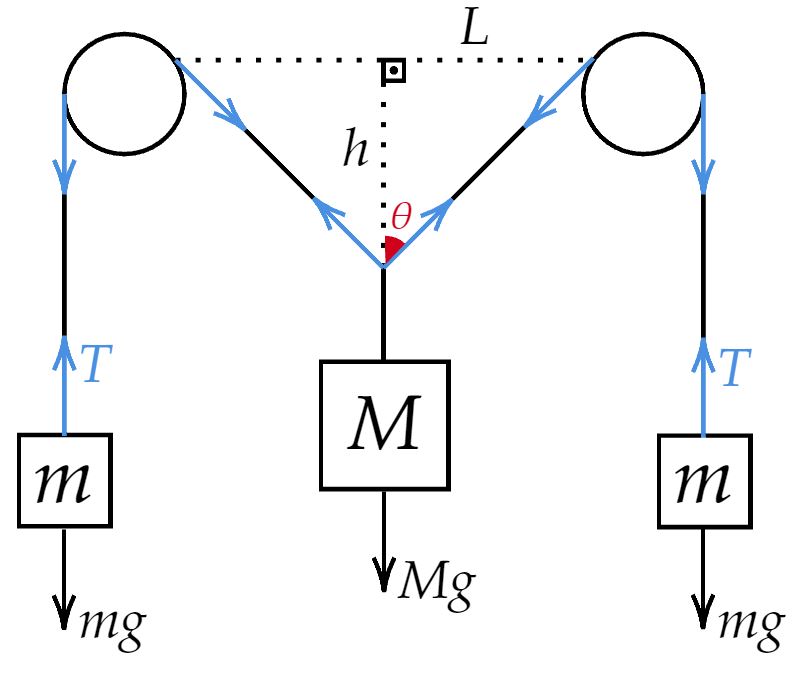 Agora, pensando exclusivamente nos blocos, podemos escrever:\begin{matrix}
Mg = 2T\cos{\theta} &,& T = mg
\end{matrix}\begin{matrix} \cos{\theta} = \dfrac{M}{2m}
\end{matrix}Analisando $ \cos{\theta} $, têm-se:\begin{matrix}
\cos{\theta} = \dfrac{h}{\sqrt{h^2 + L^2}} = \dfrac{M}{2m} \\ \\
\dfrac{h^2}{{h^2 + L^2}} = \dfrac{M^2}{4m^2} \\ \\
\boxed{h =\dfrac{ML}{\sqrt{4m^2 - M^2}}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}
Agora, pensando exclusivamente nos blocos, podemos escrever:\begin{matrix}
Mg = 2T\cos{\theta} &,& T = mg
\end{matrix}\begin{matrix} \cos{\theta} = \dfrac{M}{2m}
\end{matrix}Analisando $ \cos{\theta} $, têm-se:\begin{matrix}
\cos{\theta} = \dfrac{h}{\sqrt{h^2 + L^2}} = \dfrac{M}{2m} \\ \\
\dfrac{h^2}{{h^2 + L^2}} = \dfrac{M^2}{4m^2} \\ \\
\boxed{h =\dfrac{ML}{\sqrt{4m^2 - M^2}}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}

Ampliar Imagem
Seja $T$ a tração dos fios que estão conectados ao bloco de massa $m$ , $T'$ a tração do fio que está conectado ao bloco de massa $M$ , $\theta$ o ângulo que o fio de tração $T$ realiza com o eixo vertical que contém o ponto $Q$ e $x$ a medida do fio de tração $T$ partindo do ponto $Q$ a uma das polias.
primeiramente iremos analisar o bloco de massa $m$ , como este bloco está em equilíbrio podemos afirmar que
$\boxed{T = mg}$
Sabendo que o bloco de massa $M$ está em equilíbrio podemos dizer que
$\boxed{T' = Mg}$
Agora iremos analisar as forças no ponto $Q$ , note que na horizontal a força resultante é igual a zero , analisando a vertical iremos concluir que
$2T \cos\theta = T' = 2mg \cos\theta = Mg \implies \boxed{\cos\theta = \dfrac{M}{2m}}$
Note que $\cos\theta = \dfrac{h}{x}$
$\therefore$
$\cos\theta = \dfrac{M}{2m} = \dfrac{h}{x} \implies \boxed{x = \dfrac{2m \cdot h}{M}}$
Utilizando o Teorema de Pitágoras encontraremos a seguinte igualdade
$x^2 = L^2 + h^2 $
$= \left( \dfrac{2m \cdot h}{M} \right)^2 = L^2 + h^2 = \dfrac{4m^2 \cdot h^2}{M^2 } $
$\implies h^2 \left(\dfrac{4m^2}{M^2} - 1 \right) = L^2 = h^2 \left(\dfrac{4m^2 - M^2}{M^2} \right) $
$\implies h^2 = \dfrac{(L \cdot M)^2}{4m^2 - M^2} $
$\implies \boxed{h = \dfrac{ML}{\sqrt{4m^2 - M^2}}}$
$\textbf{Resposta : Alternativa A}$


