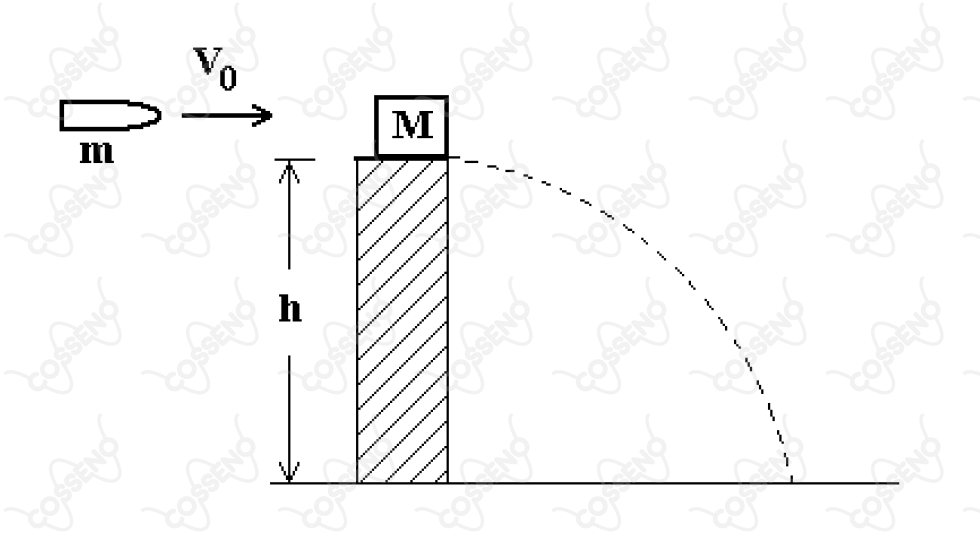
Uma bala de massa e velocidade é disparada contra um bloco de massa , que inicialmente se encontra em repouso na borda de um poste de altura , conforme mostra a figura. A bala aloja-se no bloco que, devido ao impacto, cai no solo. Sendo a aceleração da gravidade, e não havendo atrito e nem resistência de qualquer outra natureza, o módulo da velocidade com que o conjunto atinge o solo vale
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Conservação da quantidade de movimento na colisão: \begin{matrix} mV_0 + M(0) = (m+M)v \\ \fbox{$ v = \dfrac{mV_0}{(m+M)}$}
\end{matrix}Conservação da energia mecânica após a colisão: \begin{matrix} (m+M)gh + \dfrac{(m+M)v^2}{2} = \dfrac{(m+M)V^2}{2} \\ \\ V^2 = v^2 + 2gh \\ \\ \fbox{$ V = \sqrt{\left(\dfrac{mV_0}{m+M}\right)^2 + 2gh} $} \\ \\ \\ Letra \ (A)
\end{matrix}
Seja $v_{x}$ a velocidade da bala e do bloco bem depois da colisão e $v_{y}$ a velocidade vertical que o bloco atinge o solo.
Utilizando a conservação do momento linear podemos escrever que
$v_{x}(M+ m) = mv_{0} \implies v_{x} = \dfrac{mv_{0}}{M+m}$
Note que a velocidade $v_{x}$ tem direção horizontal.
Analisando o movimento de queda livre do bloco podemos concluir que
$v_{y}^2 = 2gh$
Note que a velocidade $v$ com que o conjunto atinge o solo é dado por $v = \sqrt{v_{x}^2 +v_{y}^2}$
$\therefore$
$v = \sqrt{v_{x}^2 +v_{y}^2}$
$= \boxed{v = \sqrt{\left(\dfrac{mv_{0}}{M+m}\right)^2 +2gh}}$
$\textbf{Resposta : Alternativa A}$


