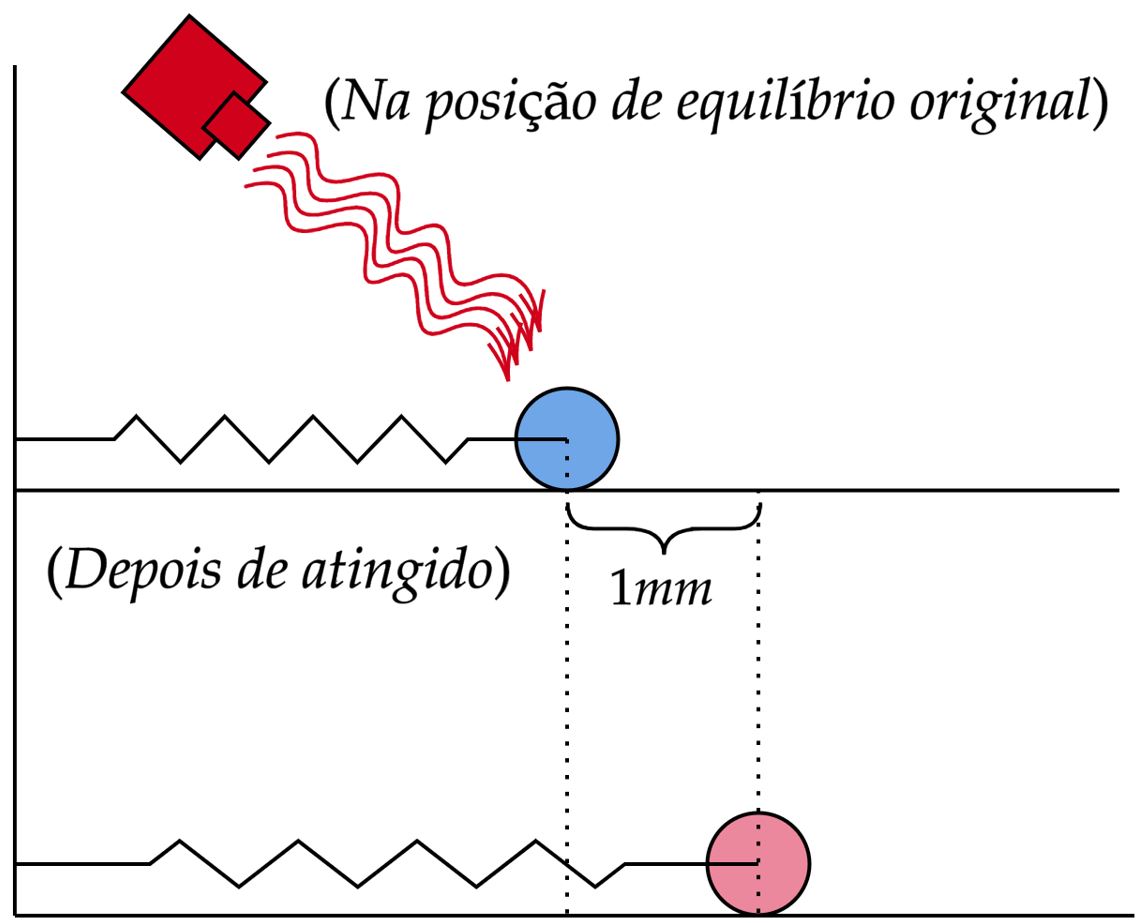
Aplica-se instantaneamente uma força a um corpo de massa preso a uma mola, e verifica-se que este passa a oscilar livremente com a freqüência angular . Agora, sobre esse mesmo corpo preso à mola, mas em repouso, faz-se incidir um feixe de luz monocromática de freqüência , de modo que toda a energia seja absorvida pelo corpo, o que acarreta uma distensão de da sua posição de equilíbrio. Determine o número de fótons contido no feixe de luz.
Constante de Planck $h = 6,6 \times 10^{-34}\ J s$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Entende-se pelo enunciado que, toda energia que provém dos fótons será convertida em energia mecânica, esta que deve ser mais precisamente convertida em energia elástica, vide a distensão. Desse modo, com conhecimento da energia de um fóton, têm-se: \begin{matrix} n \cdot E_{fóton} = E_M &\Rightarrow& n \cdot hf = {{\dfrac{Kx^2}{2}}} & (1)
\end{matrix}Continuando, o enunciado ainda informa a frequência angular, assim, como o movimento é característico de um $MHS$, constata-se que:\begin{matrix} \omega = {{\sqrt{\dfrac{K}{m}}}} &\Rightarrow& 10 = {{\sqrt{\dfrac{K}{3,3}}}} &\therefore& K = 330 \ \pu{N/m}
\end{matrix}Portanto, como a distensão $x$ é igual a $1mm$, o que equivale a $10^{-3}\pu{m}$, têm-se em $(1)$: \begin{matrix} n \cdot (6,6\times 10^{-34} \cdot 500 \times 10^{12}) = {{\dfrac{330 \cdot (10^{-3})^2}{2}}} &\therefore& n = 5 \times 10^{14} \ \text{fótons} & \tiny{\blacksquare}
\end{matrix}

Ampliar Imagem

