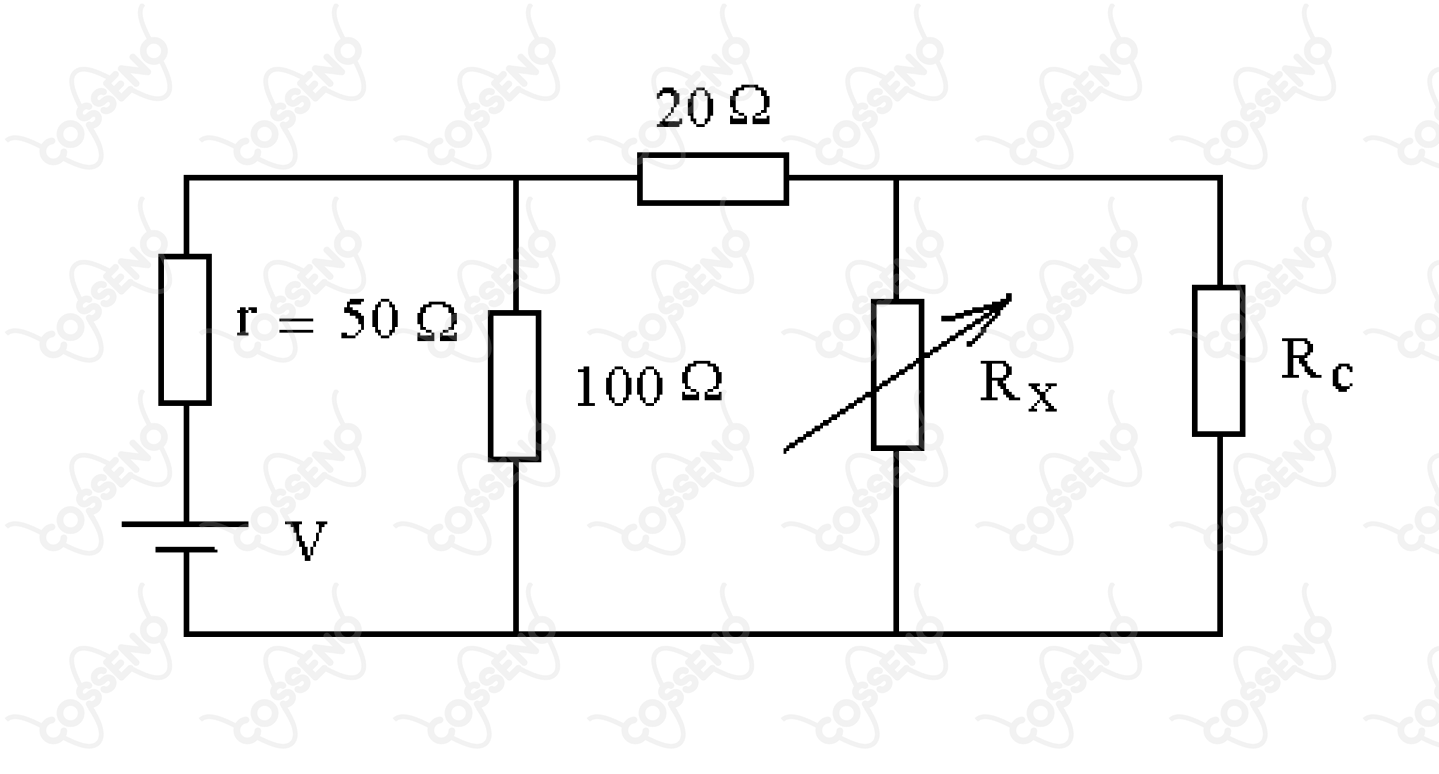
Sabe-se que a máxima transferência de energia de uma bateria ocorre quando a resistência do circuito se iguala à resistência interna da bateria, isto é, quando há o casamento de resistências. No circuito da figura, a resistência de carga varia na faixa . O circuito possui um resistor variável,, que é usado para o ajuste da máxima transferência de energia. Determine a faixa de valores de para que seja atingido o casamento de resistências do circuito.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A partir da figura do enunciado, comecemos fazendo a associação em paralelo entre $R_x$ e $R_c$, resultando no resistor equivalente $R$: \begin{matrix} R = { \dfrac{R_x \cdot R_c}{R_x \ + \ R_c}}
\end{matrix}Agora, o resistor $R$ está em série com o de $20 \ \Omega$ e em paralelo com o de $100 \ \Omega$. Nessa perspectiva, o resistor equivalente, segundo enunciado, deve apresentar mesma resistência interna da bateria, logo: \begin{matrix} r = { \dfrac{(R+ 20) \cdot 100}{(R+ 20) \ + \ 100}} &\Rightarrow& R = 80 \ \Omega &,& {{ \dfrac{R_x \cdot R_c}{R_x \ + \ R_c}}} = 80 &\therefore& R_x = { \dfrac{80\cdot R_c}{R_c \ - \ 80}}
\end{matrix}Com isso, ao variar $R_c$, temos:
$• \ R_c = 100 \ \Omega$ \begin{matrix} R_x = { \dfrac{80\cdot 100}{100 \ - \ 80}} &\therefore& R_x = 400 \ \Omega
\end{matrix}
$• \ R_c = 400\ \Omega$ \begin{matrix} R_x = { \dfrac{80\cdot 400}{400\ - \ 80}} &\therefore& R_x = 100 \ \Omega
\end{matrix}Portanto, a faixa de valores de $R_x$ para que seja atingido o casamento de resistências do circuito é: \begin{matrix} \fbox{$R_x \in [100,400] \ [\Omega]$}
\end{matrix}

