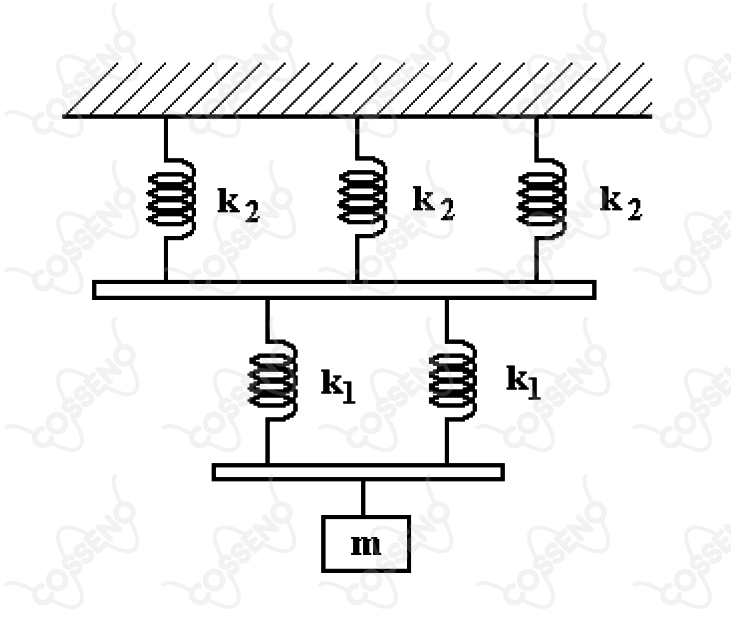
Um sistema massa-molas é constituído por molas de constantes e , respectivamente, barras de massas desprezíveis e um corpo de massa , como mostrado na figura. Determine a freqüência desse sistema.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Com conhecimento sobre $\text{Associação de Molas}$, pode-se dizer que numa associação em paralelo temos:\begin{matrix} k_{1eq} = k_1 + k_1 + k_1 &,& k_{2eq} = k_2 + k_2 \\ \\ k_{1eq} = 3k_1 && k_{2eq} = 2k_2
\end{matrix}Agora, repare que temos uma associação em série de $k_{1eq}$ e $k_{2eq}$, então:\begin{matrix} \Large{\frac{1}{K} = \frac{1}{k_{1eq}} + \frac{1}{k_{2eq}}} \\ \\ K = \Large{\frac{6k_1k_2}{3k_1 + 2k_2}}
\end{matrix}A frequência de um MHS:\begin{matrix} T = 2\pi \ \sqrt{{\dfrac{m}{K}}} &\Rightarrow& f = {\dfrac{1}{2\pi} \ \sqrt{\dfrac{K}{m}}} &\Rightarrow&
\fbox{$f = {\dfrac{1}{2\pi} \ \sqrt{\dfrac{6k_1k_2}{m(3k_1 + 2k_2)}}} $}
\end{matrix}

