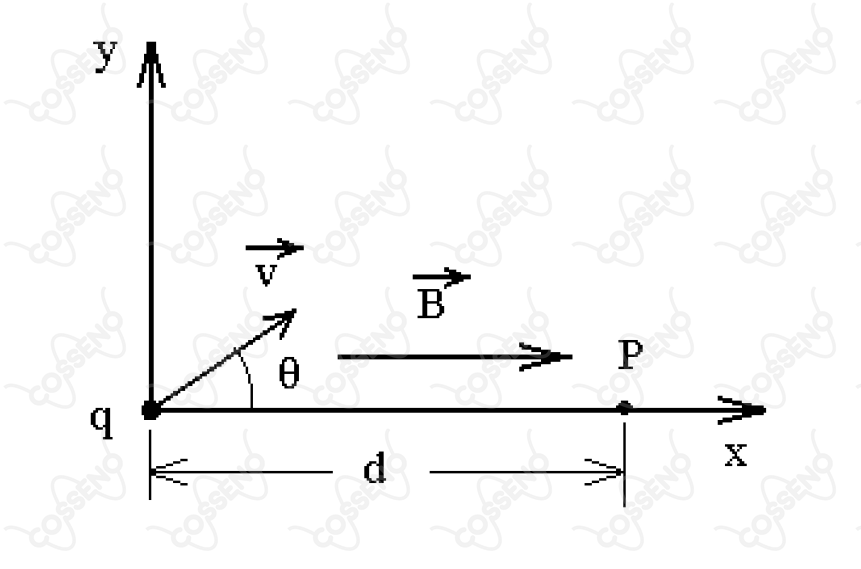
A figura mostra uma partícula de massa m e carga , numa região com campo magnético constante e uniforme, orientado positivamente no eixo . A partícula é então lançada com velocidade inicial no plano , formando o ângulo indicado, e passa pelo ponto , no eixo , a uma distância do ponto de lançamento. Assinale a alternativa correta.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Começando por decompor a velocidade, nota-se pela regra da mão direita que a componente $v\cos{\theta}$ está paralela ao campo magnético, ou seja, não produz força. Por outro lado, a componente $v\sin{\theta}$ produz, força essa para dentro da tela, que será responsável por um movimento helicoidal da partícula, veja:
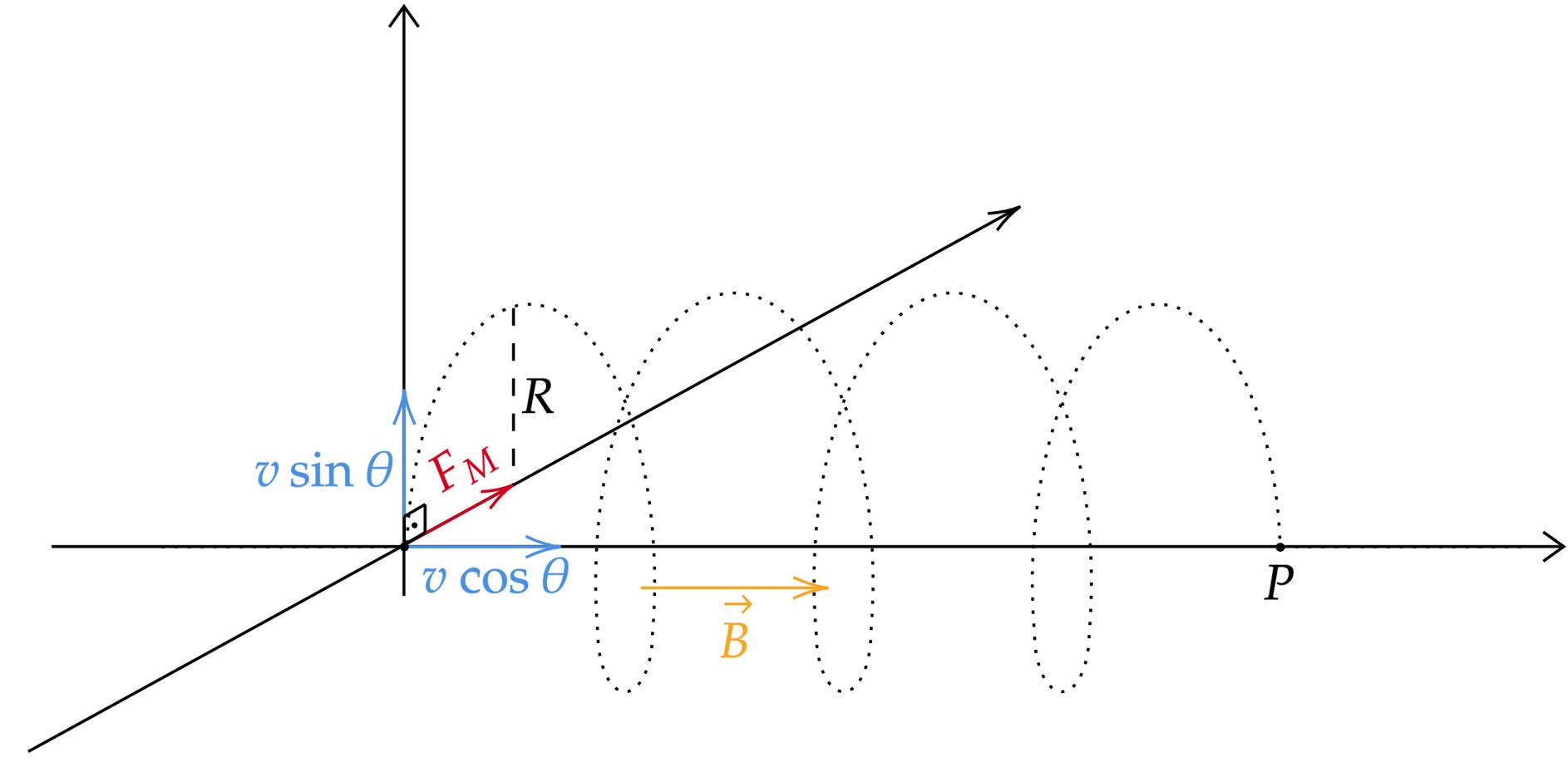 Analisando cada alternativa:
$• \ \text{Alternativa (A):}$ $\color{#3368b8}{\text{Correta}}$
Pensando na resultante centrípeta, podemos escrever:\begin{matrix}
\dfrac{m(v\sin{\theta})^2}{R} = Bq(v\sin{\theta})
\end{matrix}Em busca de $R$, podemos tentar encontrá-lo a partir do período do movimento, no caso, o tempo que a partícula leva até $P$ a partir do movimento horizontal (este uniforme):\begin{matrix}
d = (v\cos{\theta}) \Delta t
\end{matrix}Agora, pensando no período que a partícula leva para voltar ao eixo $x$, isto é, voltar a $P$:\begin{matrix}\Delta t = \dfrac{2\pi R}{v\sin{\theta}}
\end{matrix}Relacionando os dois resultados anteriores:\begin{matrix} R = \dfrac{d\sin{\theta} }{2\pi \cos{\theta}}
\end{matrix}Substituindo o resultado acima na primeira expressão:\begin{matrix}\boxed{dqB = 2\pi mv \cos{\theta}}
\end{matrix}$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Incorreta}}$
A força magnética não realiza trabalho neste caso - ela é perpendicular o movimento - assim, sendo o sistema conservativo, a energia cinética é a mesma.
$• \ \text{Alternativa (C):}$ $\color{orangered}{\text{Incorreta}}$
Para $\theta = 0º$, a componente da velocidade é estritamente horizontal, paralela ao campo magnético. Desse modo, o movimento deve ser retilíneo e uniforme, visto que não atuam forças para acelerar o sistema.
$• \ \text{Alternativa (D):}$ $\color{orangered}{\text{Incorreta}}$
Conforme resultados anteriores: \begin{matrix} \Delta t = \dfrac{2\pi R}{v\sin{\theta}} &,& (v\sin{\theta}) = \dfrac{BqR}{m}
\end{matrix}Portanto,\begin{matrix} \Delta t = \dfrac{2\pi m}{Bq}
\end{matrix}$• \ \text{Alternativa (E):}$ $\color{orangered}{\text{Incorreta}}$
Sendo $\theta \ne 0º$, o campo magnético deve produzir uma força magnética responsável por um movimento helicoidal da partícula. Consequentemente, o campo irá atribuir uma aceleração centrípeta ao sistema.
\begin{matrix}Letra \ (A)
\end{matrix}
Analisando cada alternativa:
$• \ \text{Alternativa (A):}$ $\color{#3368b8}{\text{Correta}}$
Pensando na resultante centrípeta, podemos escrever:\begin{matrix}
\dfrac{m(v\sin{\theta})^2}{R} = Bq(v\sin{\theta})
\end{matrix}Em busca de $R$, podemos tentar encontrá-lo a partir do período do movimento, no caso, o tempo que a partícula leva até $P$ a partir do movimento horizontal (este uniforme):\begin{matrix}
d = (v\cos{\theta}) \Delta t
\end{matrix}Agora, pensando no período que a partícula leva para voltar ao eixo $x$, isto é, voltar a $P$:\begin{matrix}\Delta t = \dfrac{2\pi R}{v\sin{\theta}}
\end{matrix}Relacionando os dois resultados anteriores:\begin{matrix} R = \dfrac{d\sin{\theta} }{2\pi \cos{\theta}}
\end{matrix}Substituindo o resultado acima na primeira expressão:\begin{matrix}\boxed{dqB = 2\pi mv \cos{\theta}}
\end{matrix}$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Incorreta}}$
A força magnética não realiza trabalho neste caso - ela é perpendicular o movimento - assim, sendo o sistema conservativo, a energia cinética é a mesma.
$• \ \text{Alternativa (C):}$ $\color{orangered}{\text{Incorreta}}$
Para $\theta = 0º$, a componente da velocidade é estritamente horizontal, paralela ao campo magnético. Desse modo, o movimento deve ser retilíneo e uniforme, visto que não atuam forças para acelerar o sistema.
$• \ \text{Alternativa (D):}$ $\color{orangered}{\text{Incorreta}}$
Conforme resultados anteriores: \begin{matrix} \Delta t = \dfrac{2\pi R}{v\sin{\theta}} &,& (v\sin{\theta}) = \dfrac{BqR}{m}
\end{matrix}Portanto,\begin{matrix} \Delta t = \dfrac{2\pi m}{Bq}
\end{matrix}$• \ \text{Alternativa (E):}$ $\color{orangered}{\text{Incorreta}}$
Sendo $\theta \ne 0º$, o campo magnético deve produzir uma força magnética responsável por um movimento helicoidal da partícula. Consequentemente, o campo irá atribuir uma aceleração centrípeta ao sistema.
\begin{matrix}Letra \ (A)
\end{matrix}

Ampliar Imagem


