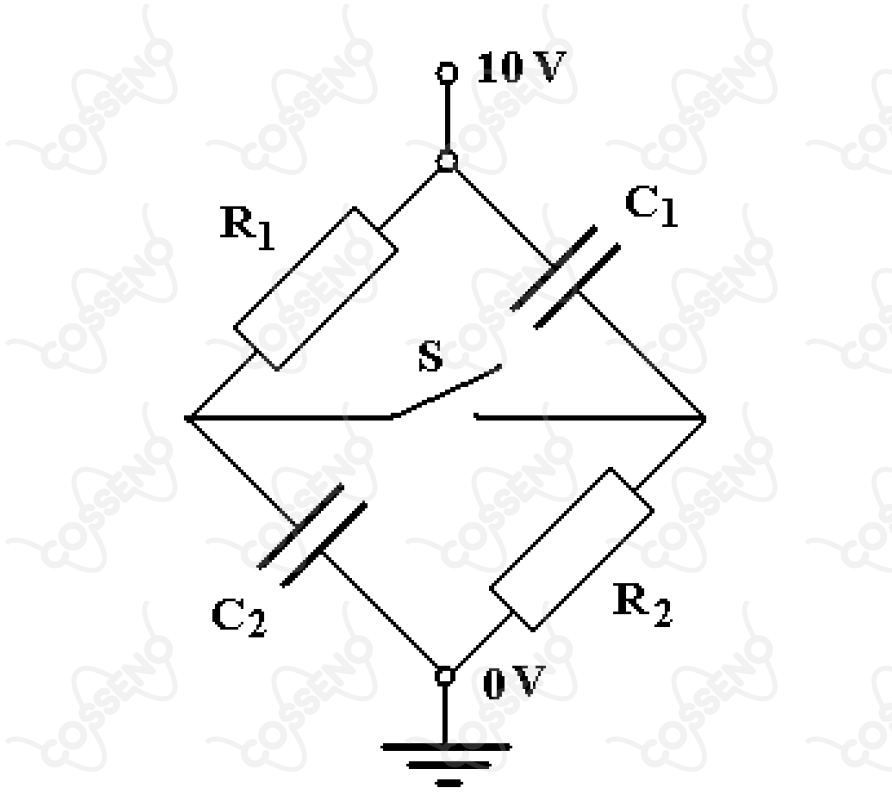
O circuito da figura é composto de duas resistências, $R_1 = 1,0 \times 10^3\ \Omega$ e $R_2 = 1,5 \times 10^3\ \Omega$, respectivamente, e de dois capacitores, de capacitâncias $C_1 = 1,0 \times 10^{-9}\ F$ e $C_2 = 2,0 \times 10^{-9}\ F$, respectivamente, além de uma chave $S$, inicialmente aberta. Sendo fechada a chave $S$, a variação da carga $\Delta Q$ no capacitor de capacitância $C_1$, após determinado período, é de
Estando os capacitores carregados em ambas as situações, isto é, regime estacionário, eles atuarão como circuitos abertos com a chave aberta ou fechada, tendo-se assim dois casos:
$• \ \text{Chave Aberta:}$ Nessa configuração ambos os capacitores estão sujeitos a mesma $ddp$ $(\Delta V)$ de $10 \ V$, nesse caso, pela expressão da capacitância, temos: \begin{matrix} Q = C.\Delta V &\Rightarrow& \fbox{$Q_i =10 \cdot 10^{-9} \ \pu{C}$}
\end{matrix}
$• \ \text{Chave Fechada:}$ Já ao fechar a chave, existe corrente passando pelo sistema, da $\text{lei de ohm generalizada}$, têm-se: \begin{matrix} \Delta V = (R_1 + R_2)i &\therefore& i = {{\dfrac{1}{250} }} \ A
\end{matrix}A diferença de potencial em $R_2$:\begin{matrix} V_{R_2} - 0 = R_2.i &\therefore& V_{R_2} = 6 \ \pu{V}
\end{matrix}Dessa forma, a diferença de potencial em $C_1$:\begin{matrix} \Delta V_{C_1} =10 - V_{R_2} = 4 \ \pu{V} &,& Q_f = C_1 \Delta V_{C_1} &\therefore& \fbox{$Q_f =4\cdot 10^{-9} \ \pu{C}$}
\end{matrix}Por fim, a variação de carga que ocorre no capacitor $C_1$:\begin{matrix} \Delta Q = Q_f -Q_i &\therefore& \fbox{$\Delta Q =-6\cdot 10^{-9} \ \pu{C}$}
\end{matrix}\begin{matrix} Letra \ (B)
\end{matrix}
