De acordo com o enunciado, pode-se obter a seguinte figura: 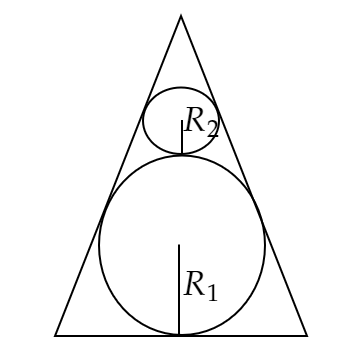Com isso, pode-se demonstrar a partir de um pouco de trigonometria, que o raio $R_{1}$ é igual a um terço da altura, basta usar a tangente de $30^\circ$ e seno de $60^\circ$. Com isso, veja que do ponto mais baixo da circunferência $2$ até o restante da altura do triângulo retângulo, falta $\frac{h}{3}$, logo o raio $R_{2}$ é $\frac{h}{9},$ isso fica claro quando você traça um segmento de reta para fechar outro triângulo na circunferência $2$. Logo, $$\dfrac{R_{1} - R_{2}}{h} = \dfrac{2}{9}.$$