Vamos começar esboçando as duas situações: 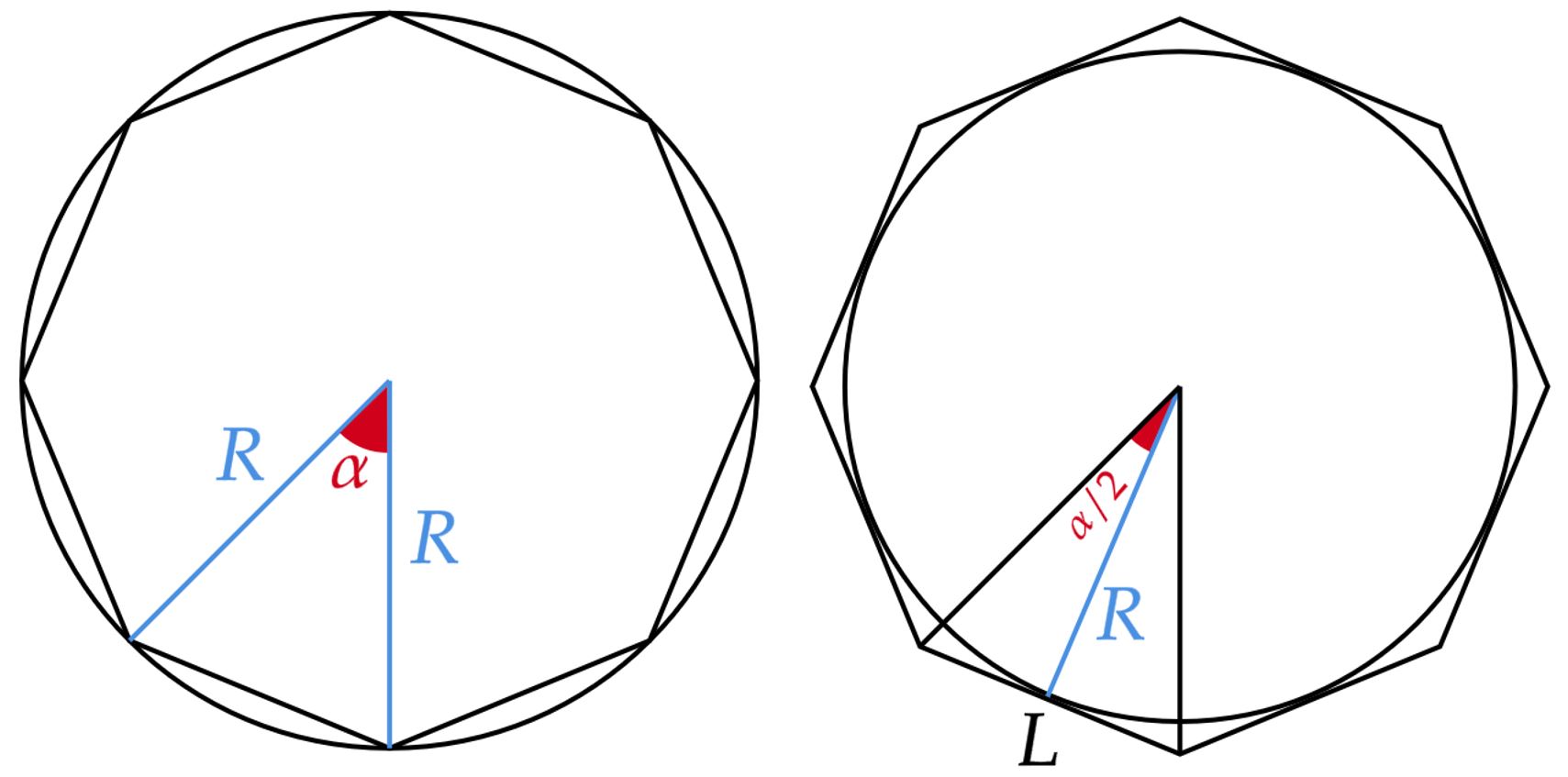Pensando em $P_1$, observe que sua área não é nada mais que oito triângulos idênticos ao da imagem, tal que:\begin{matrix} A_1 = 8 \left( \dfrac{R^2\sin{\alpha}}{2}\right) \end{matrix}Como $\alpha$ é $45º$, visto que $\alpha = 360º/8$, têm-se:\begin{matrix}\boxed{ A_1 = 2R^2\sqrt{2}} \end{matrix}Analogamente, para $P_2$, têm-se:\begin{matrix} A_2 = 8 \left( \dfrac{L R}{2}\right) \end{matrix}Veja que precisamos colocar $L$, para isso, vamos pensar na tangente de $\alpha/2$:\begin{matrix} \tan{(\alpha/2)} = \dfrac{L}{2R} &,& \tan{(\alpha/2)} = \dfrac{\sin{\alpha}}{\cos{\alpha} + 1} \end{matrix}Então,\begin{matrix} \tan{(\alpha/2)} = \dfrac{\sqrt{2}}{2+ \sqrt{2}} &\Rightarrow& L =\dfrac{2R\sqrt{2}}{2+ \sqrt{2}} \end{matrix}Portanto,\begin{matrix}\boxed{ A_2 = 8 \left( \dfrac{R^2\sqrt{2}}{2+ \sqrt{2}} \right)} \end{matrix}Conclui-se que razão é:\begin{matrix}\dfrac{A_1}{A_2} = \dfrac{2R^2\sqrt{2}}{8 \left( \dfrac{R^2\sqrt{2}}{2+ \sqrt{2}} \right)} = \dfrac{(2+\sqrt{2})}{4}&\tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (E) \end{matrix} $\color{orangered}{\text{Obs:}}$\begin{matrix} \tan{(\alpha/2)} = \dfrac{\sin{(\alpha/2)} }{\cos{(\alpha/2)} } \end{matrix}Em que:\begin{matrix} \sin{(\alpha)} &=& 2\sin{(\alpha/2)}\cos{(\alpha/2)} \\ \cos{(\alpha)} &=& 2\cos^2{(\alpha/2)} -1 \end{matrix}Substituindo os resultados acima:\begin{matrix} \tan{(\alpha/2)} = \dfrac{\sin{\alpha}}{\cos{\alpha} + 1} \end{matrix}