A princípio, vamos pensar na base hexagonal, sabemos que ela é um hexágono regular, então podemos esboçar: 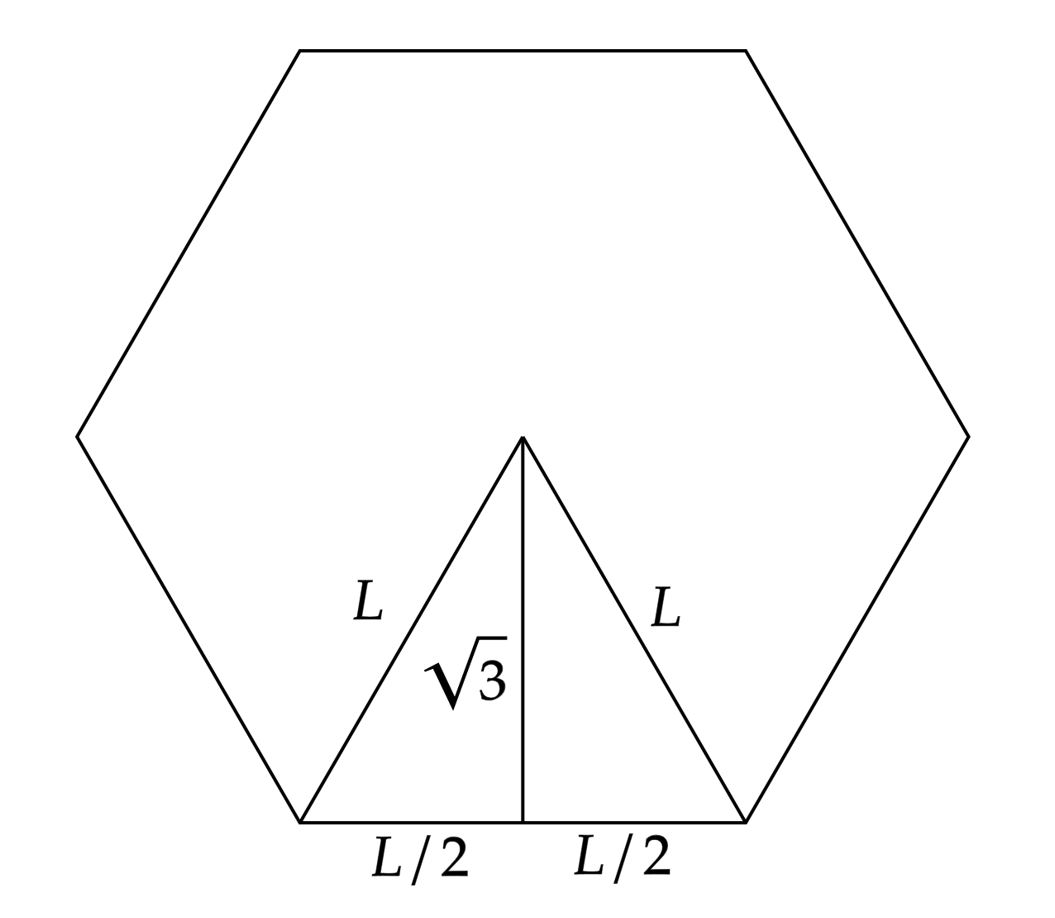Repare que podemos dividir o hexágono em seis triângulos equiláteros de lado $L$, desse modo, o apótema é a altura desses triângulos. Nesse sentido, para encontrar $L$, basta saber a altura de um triângulo equilátero:\begin{matrix} \dfrac{L\sqrt{3}}{2} = \sqrt{3} &\therefore& L = 2 \end{matrix}$\color{orangered}{\text{Obs:}}$ Você poderia aplicar Pitágoras, ou utilizar os conceitos de trigonometria, além de diversas outras formas. Pensando no volume do tronco, pode-se escrever sua fórmula característica como:\begin{matrix} V_T = \dfrac{H_T}{3} \left( B + b + \sqrt{Bb}\right) \end{matrix}Em que $B$ é a área da base maior, assim como $b$ a área da base menor. Analogamente, pensando em relacionar as áreas da base com as alturas, podemos aplicar uma semelhança:\begin{matrix} \left( \dfrac{b}{B}\right) = \left( \dfrac{1}{\sqrt{2}}\right)^2 &\therefore& B = 2b \end{matrix}Encontrar $B$ não é difícil, podemos fazer:\begin{matrix}B = 6\left( \dfrac{L^2\sqrt{3}}{4}\right) = 6\sqrt{3} &\Rightarrow& b = 3\sqrt{3} \end{matrix}Portanto, substituindo nossos resultados na expressão do tronco: \begin{matrix} V_T = \dfrac{H_T}{3} \left( 3b + b\sqrt{2}\right) = 1 \\ \\ H_T (3\sqrt{3} + \sqrt{6}) = 1 \\ \\ \boxed{H_T = \dfrac{ (3\sqrt{3} - \sqrt{6}) }{21}} \\ \\ Letra \ (C) \end{matrix}