Pensando num polígono de $n$ lados, assim como o apótema e o comprimento da base, temos: 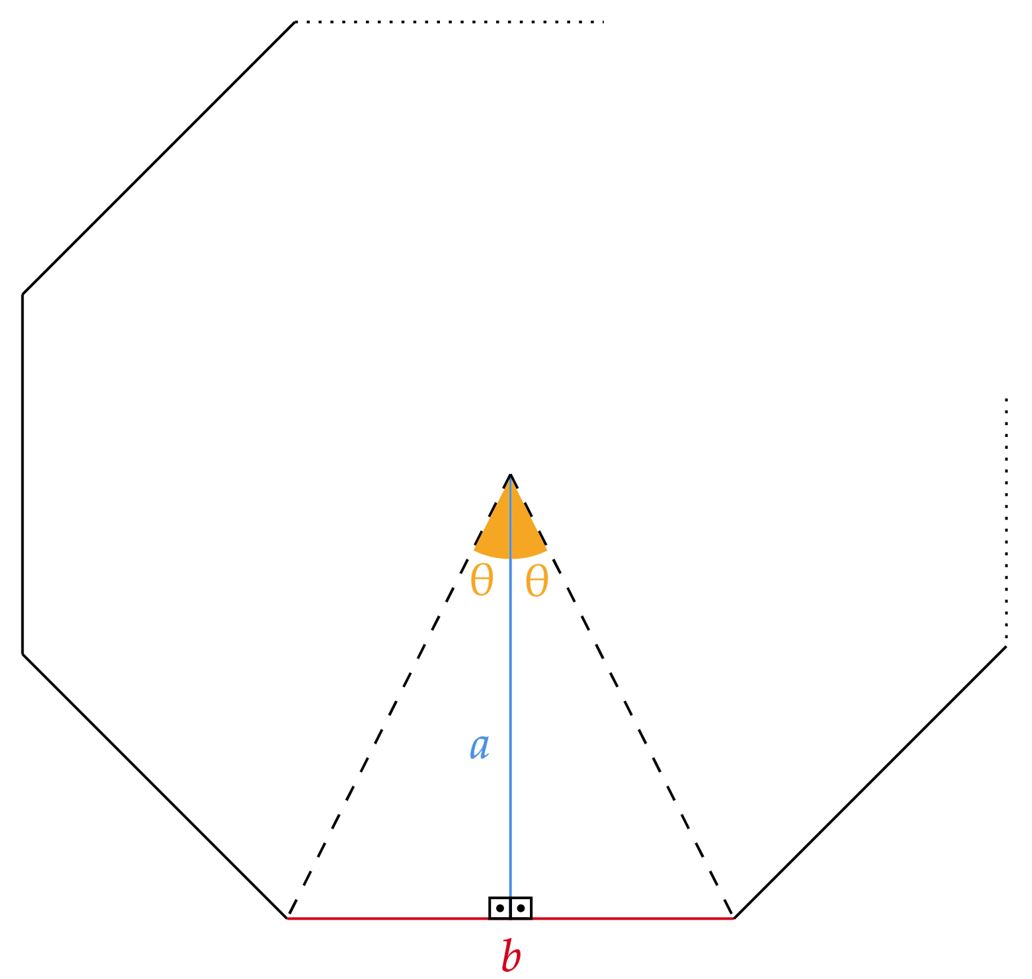Ao analisar a situação, nota-se que: \begin{matrix} 2\theta_n = \dfrac{2\pi}{n} &\Rightarrow& \theta_n = \dfrac{\pi}{n} \end{matrix}Observe que podemos relacionar $a$, $b$ e $n$ a partir da tangente de $\theta$, em que: \begin{matrix} \tan{\theta} = \dfrac{1}{2}\cdot \dfrac{b}{a} \end{matrix}Conforme as desigualdades, para $b_n \le a_n$, devemos ter: \begin{matrix} \tan{\left( \dfrac{\pi}{n}\right)} = \dfrac{1}{2}\cdot \dfrac{b_n}{a_n} \le \dfrac{1}{2} &\Rightarrow& \dfrac{\pi}{n} \le \arctan{\dfrac{1}{2}} < \ \dfrac{\pi}{6} &\therefore& n >6 \end{matrix}Já para $b_{n-1} > a_{n-1}$:\begin{matrix} \tan{\left( \dfrac{\pi}{n-1}\right)} = \dfrac{1}{2}\cdot \dfrac{b_{n-1}}{a_{n-1}} > \dfrac{1}{2} &\Rightarrow& \dfrac{\pi}{n-1} > \arctan{\dfrac{1}{2}} > \ \dfrac{\pi}{8} &\therefore& n <9 \end{matrix}Conclui-se então:\begin{matrix}\boxed{6<n<9} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}$\color{orangered}{\text{Obs:}}$ Não se esqueça que $n$ é um inteiro, afinal, ele representa os lados de um polígono. Analogamente, para as desigualdades acerca dos ângulos, eles devem ser na forma $\pi/k$ em que $k$ é um inteiro. Por fim, ressalta-se que para tangente, quando menor o ângulo, menor é a tangente, logo, pensando em ângulos notáveis, rapidamente, pode-se supor as desigualdades listadas.