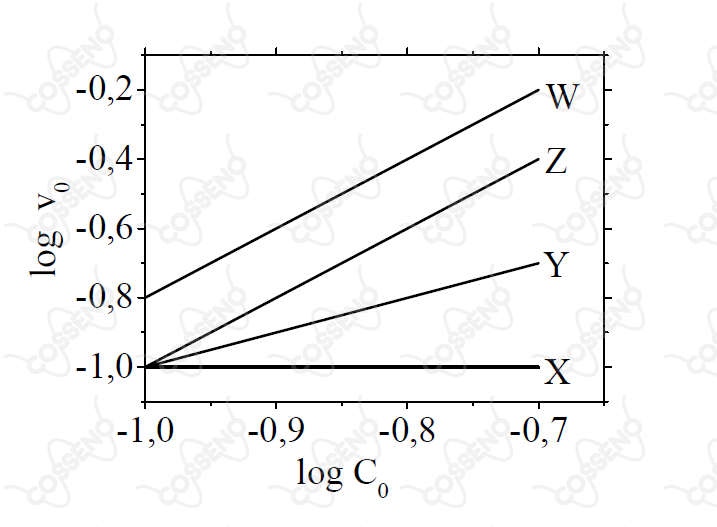
Considere quatro séries de experimentos em que quatro espécies químicas ( e ) reagem entre si, à pressão e temperatura constantes. Em cada série, fixam-se as concentrações de três espécies e varia-se a concentração () da quarta. Para cada série, determina-se a velocidade inicial da reação () em cada experimento. Os resultados de cada série são apresentados na figura, indicados pelas curvas e , respectivamente. Com base nas informações fornecidas, assinale a opção que apresenta o valor CORRETO da ordem global da reação química.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, entende-se há quatro reagentes, estes que estão presentes no gráfico. Além disso, percebe-se que a partir dos coeficientes angulares das retas, pode-se relacionar a velocidade inicial da reação com a respectiva concentração da espécie analisada, assim, seja um coeficiente arbitrário $\tan{\alpha}$, dele têm-se: \begin{matrix} \tan{\alpha} = {{\dfrac{\log{v_0}}{\log{C_0}}}} = \log_{C_0}^{\large{v_0}} &\therefore& v_0 ={C_0}^{\tan{\alpha}}
\end{matrix}Nessa perspectiva, analisando o coeficiente angular de cada reta, encontra-se a ordem de decréscimo da concentração de cada regente, veja: \begin{matrix}
\tan{W} = {{\dfrac{(-0,2 + 0,8)}{(-0,7+1,0)}}} = 2 &\Rightarrow& V_{0_W} = [W]^2& \text{(segunda ordem)} \\ \\
\tan{Z} = {{\dfrac{(-0,4 + 1,0)}{(-0,7+1,0)}}} = 2 &\Rightarrow& V_{0_Z} = [Z]^2& \text{(segunda ordem)} \\ \\
\tan{Y} = {{\dfrac{(-0,7 + 1,0)}{(-0,7+1,0)}}} = 1 &\Rightarrow& V_{0_Y} = [Y]^1& \text{(primeira ordem)} \\ \\
\tan{X} \approx {{\dfrac{(0)}{(-0,7+1,0)}}} \approx 0 &\Rightarrow& V_{0_X}= [X]^0& \text{(ordem zero)}
\end{matrix}Concluí-se que a velocidade da reação independe da concentração de $X$, todavia, ela depende das demais espécies, e estas já sabemos a ordem. Desse modo, a equação de velocidade da reação global deve ser: \begin{matrix} v &=& k \cdot [X]^0
\cdot [Y]^1 \cdot [W]^2 \cdot [Z]^2 & \text{(reação global de quinta ordem)}
\end{matrix}
\begin{matrix} Letra \ (C)
\end{matrix}

