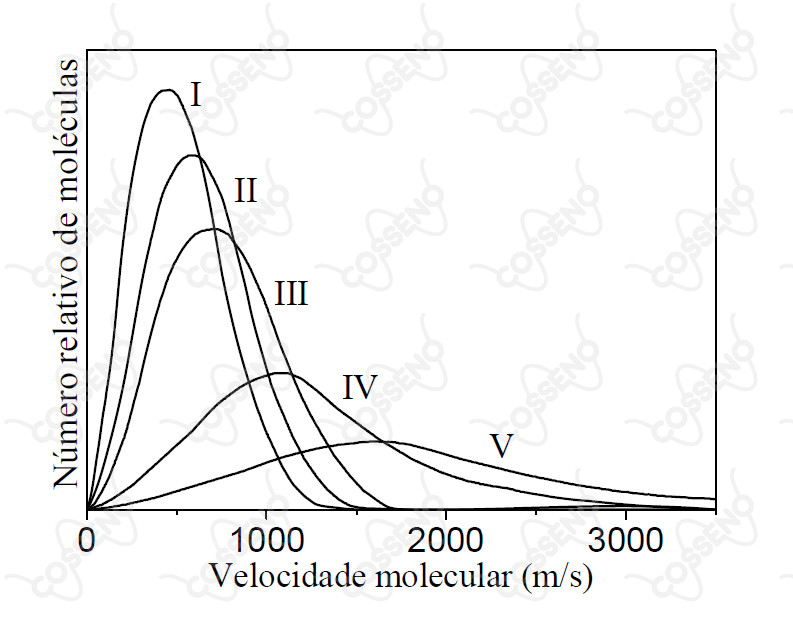
A figura mostra cinco curvas de distribuição de velocidade molecular para diferentes gases (I, II, III, IV e V) a uma dada temperatura. Assinale a opção que relaciona CORRETAMENTE a curva de distribuição de velocidade molecular a cada um dos gases.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, deve-se ter conhecimento acerca de cinética química, mais especificamente, energia cinética média dos gases. Dessa forma, podemos escrever:
\begin{matrix} E_{c_M} = \dfrac{f}{2} \cdot nRT &\Rightarrow& \dfrac{mV^2}{2} = \dfrac{f}{2} \cdot \dfrac{mRT}{M} &\therefore& \fbox{$V^2 = K {\dfrac{f}{M}}$}
\end{matrix}
\begin{matrix} f: \text{constante de atomicidade} & ,& M: \text{massa molar} &,& K = RT \end{matrix}
$\color{orangered}{Obs:}$ Estaremos admitindo que a temperatura será, em algum momento, constante.
Veja que, a velocidade ao quadrado varia conforme a atomicidade da molécula e sua massa molecular. Com isso, sabido que para moléculas monoatômicas $(He)$ o coeficiente é igual a três, para diatômicas $(O_2 \ , \ N_2 \ e \ H_2)$ é igual a cinco, e para triatômicas igual a sete, temos:
$• \ \text{Monoatômicas (f = 3)}$
\begin{matrix} He: 4u &\Rightarrow & \fbox{$V_{He}^2 = K {\dfrac{3}{4}}$}
\end{matrix}
$• \ \text{Diatômicas (f = 5)}$
\begin{matrix} O_2 : 32u &\Rightarrow & \fbox{$V_{O_{2}}^2 = K{\dfrac{5}{32}}$} &&,&& N_2 : 28u & \Rightarrow & \fbox{$V_{N_{2}}^2 = K {\dfrac{5}{28}}$} &&,&& H_2 : 2u & \Rightarrow & \fbox{$V_{H_{2}}^2 = K {\dfrac{5}{2}}$}\end{matrix}
$• \ \text{Triatômicas (f = 7)}$
\begin{matrix} H_2O : 18u&\Rightarrow & \fbox{$V_{H_2O}^2 = K {\dfrac{1}{2}}$}
\end{matrix}
Nessa perspectiva, podemos inferir:
\begin{matrix} V_{O_{2}} < V_{N_{2}} <V_{H_2O} < V_{He} < V_{H_{2}}
\end{matrix}
Agora, basta olhar o gráfico, repare na velocidade das moléculas, não é difícil perceber que:
\begin{matrix} I = O_{2} &,& II = {N_{2}} &,& III = {H_2O} &,& IV = {He} &,& V = {H_{2}}
\end{matrix}
\begin{matrix} Letra \ (B)
\end{matrix}
A análise pode ser feita pela equação da velocidade de uma molécula de gás ideal (Sendo $k$ a constante de Boltzmann, $T$ a temperatura e $m$ a massa da molécula do gás):
\begin{align*}
v = \sqrt{\frac{3kT}{m}}
\end{align*}
Quanto maior a massa, menor a velocidade.


