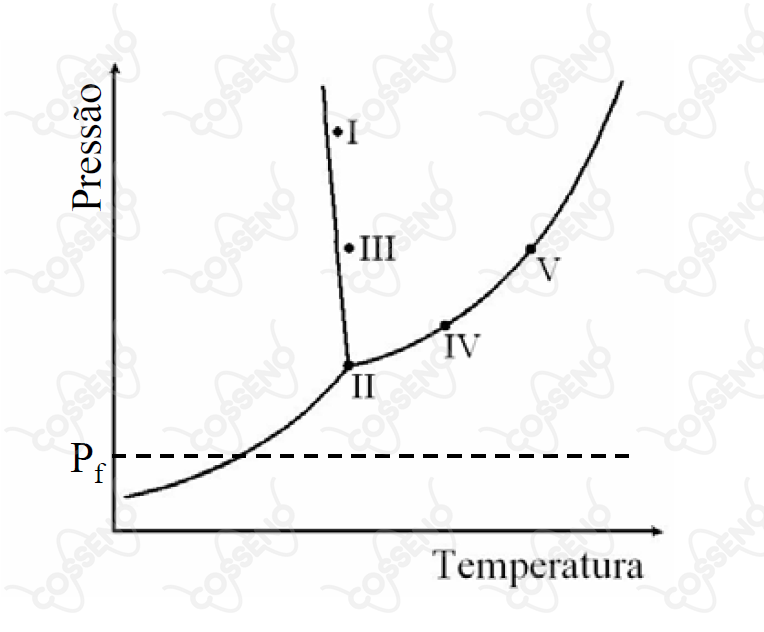
O diagrama de fases da água está representado na figura. Os pontos indicados (I, II, III, IV e V) referem-se a sistemas contendo uma mesma massa de água líquida pura em equilíbrio com a(s) eventual(ais) fase(s) termodinamicamente estável(eis) em cada situação. Considere, quando for o caso, que os volumes iniciais da fase vapor são iguais. A seguir, mantendo-se as temperaturas de cada sistema constantes, a pressão é reduzida até . Com base nestas informações, assinale a opção que apresenta a relação ERRADA entre os números de mol de vapor de água presentes nos sistemas, quando a pressão é igual a .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Interpretação I: Volumes de matéria iguais}$
Segundo enunciado, sabemos que a massa de água líquida é a mesma, isto é, o número de mols na fase líquida é o mesmo. Ademais, o enunciado também informa que os volumes iniciais das fases gasosas são os mesmos, assim, o número de mols na fase gasosa também é o mesmo nos demais sistemas em início. Nessa perspectiva, a priori, temos:
\begin{matrix} \text{I:} \ \ n_{(l)} &,& \text{II:} \ \ n_{(l)} + n_{(v)} + n_{(s)} &,& \text{III:} \ \ n_{(l)} &,& \text{IV:} \ \ n_{(l)} + n_{(v)} &,& \text{V:} \ \ n_{(l)} + n_{(v)}
\end{matrix} Atente que os pontos são:
\begin{matrix} \text{I:} & \text{Fase Líquida} &,& \text{II:} & \text{Ponto Triplo} &,& \text{III:} & \text{Fase Líquida} &,& \text{IV:} & \text{Eq. Líquido-Gás} &,& \text{V:} & \text{Eq. Líquido-Gás}
\end{matrix}
Repare que, o processo isotérmico descrito é apenas uma forma de transformar tudo em gás, o número de mols total claramente não irá variar, e como tudo será mol de vapor, têm-se nesse contexto a relação:
\begin{matrix} n_{(II)} > n_{(IV)}=n_{(V)} > n_{(I)} = n_{(III)} \\ \\ Letras \ (A) \ e \ (E)
\end{matrix}
$• \ \text{Interpretação II: Volumes dos sistemas iguais}$
Vide a interpretação anterior, ainda sabemos que o número de mols na fase líquida é o mesmo. Todavia, o número de mols das fases gasosas agora é diferentes, da equação geral dos gases teremos a proporção: \begin{matrix} n \varpropto \dfrac{P}{T} &\Rightarrow&
n_{(v_{II})} > n_{(v_{IV})} \approx n_{(v_{V})}
\end{matrix}
Veja que, é uma missão bem complicada estimar a desigualdade (quiçá igualdade) de $IV$ e $V$. Dessa forma, analogamente ao raciocínio anterior, temos a $possibilidade$ da $(E)$ estar correta, o que nos daria: \begin{matrix} Letra \ (A)
\end{matrix}

23:27 30/03/2022
Pequeno detalhe na primeira interpretação: n3<n4, pois no ponto IV além de haver a fase de vapor (nv), ainda há a fase líquida (nl).

01:41 31/03/2022
Obrigado, Augusto! Corrigi aqui, acabou faltando atenção na hora de escrever.
