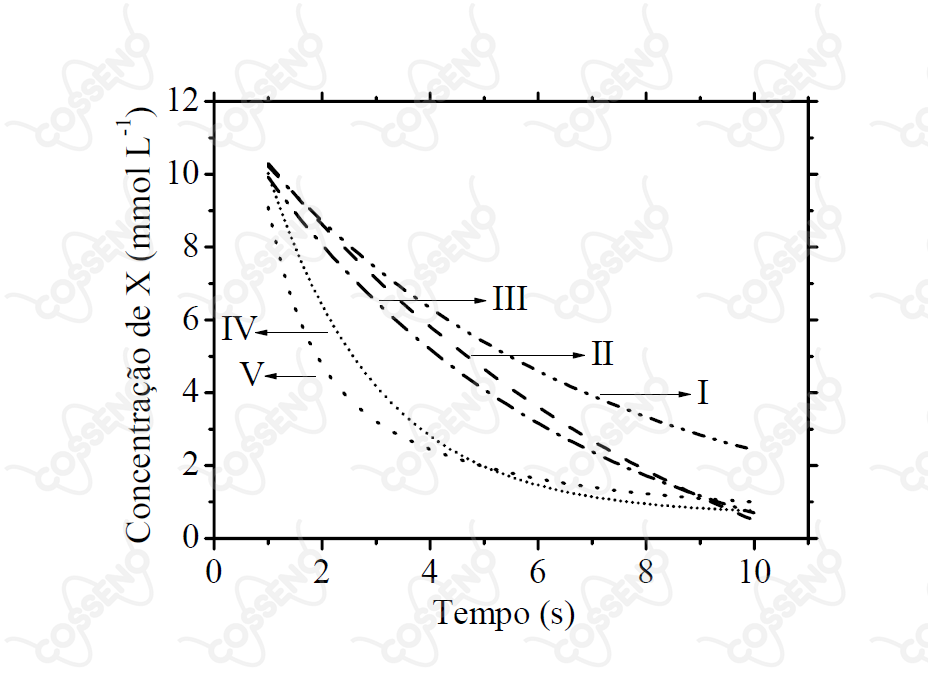
A figura apresenta cinco curvas (I, II, III, IV e V) da concentração de uma espécie em função do tempo. Considerando uma reação química hipotética representada pela equação , assinale a opção CORRETA que indica a curva correspondente a uma reação química que obedece a uma lei de velocidade de segunda ordem em relação à espécie .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Em problemas gráficos de cinética química, é válido lembrar que reações de primeira ordem possuem linha reta para os gráficos de: $$ln[X] \times t$$
Enquanto isso, reações de segunda ordem formam uma linha reta em $$\frac{1}{[X]} \times t$$
Assim, a curva V é a única que atende a essas condições.
Com conhecimento que a lei de velocidade da reação é de segunda ordem, pode-se escrever:\begin{matrix}
-\dfrac{\Delta \ce{[X]}}{\Delta t} =\ce{k [X]^2}
\end{matrix}Agora, caso se conheça a função de $\ce{X} \times \ce{Tempo}$ numa reação de segunda ordem em $\ce{X}$ o problema está resolvido. Contudo, não é recorrente lembrar que o resultado é uma hipérbole retangular, por isso - caso possível -, é interessante integrar. Veja como é prático:$$
-\dfrac{d\ce{[X]}}{\ce{[X]^2}} =\ce{k } \cdot dt \ \ \rightarrow \ \ (-1)\int_{0}^{t} {d\ce{[X]}}\cdot {\ce{[X]^{-2}}} = \ce{k } \int_{0}^{t} dt \ \ \therefore \ \ \ce{[X]} \cdot t = \dfrac{1}{k}$$Com isso, resta-nos utilizar o gráfico, vejamos a curva $\text{V}$:\begin{matrix}
\text{V}: & \begin{cases} t = 2 &\Rightarrow& \ce{[X]} = 4 \\ t = 4 &\Rightarrow& \ce{[X]} = 2 \end{cases} &\therefore& \dfrac{1}{k} = 8
\end{matrix}Portanto, nota-se que $\text{V}$ corresponde a um gráfico possível, diferente dos demais, estes que não respeitam a equação $ \ce{[X]} \cdot t = 1/k$.\begin{matrix}Letra \ (E)
\end{matrix}$\color{orangered}{\text{Obs:}}$ $$\int_{0}^{t} {d\ce{[X]}}\cdot {\ce{[X]^{n}}} = \dfrac{\ce{[X]^{n + 1 }}}{n + 1} \ \ \forall \ \ n \ne -1$$


