Pela situação descrita no enunciado, pode-se esboçar um circuito como: 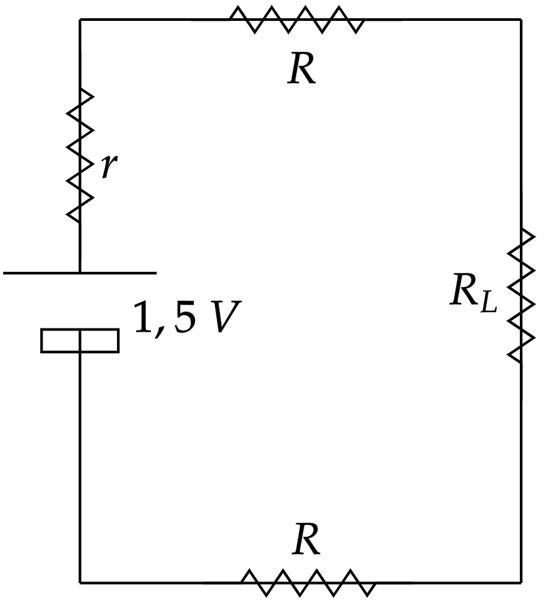A partir da $\text{Segunda Lei de Ohm}$ as resistências $R$ dos filamentos são dadas por: \begin{matrix} R = {{\dfrac{\rho \cdot L}{A}}} = {{\dfrac{(1,7.10^{-8}) \cdot 2}{\pi (0,75\cdot 10^{-3})^2}}} &\therefore& R \approx 0,019 \ \Omega \end{matrix}Com conhecimento da potência e tensão nominais da lâmpada, a resistência da lâmpada é: \begin{matrix} Pot = {\dfrac{(\Delta V)^2}{R_L}} &\therefore& R_L = 0,\overline{3} \ \Omega \end{matrix}Segundo o gerador em curto-circuito, pela corrente fornecida é possível encontrar a resistência interna da pilha, veja: \begin{matrix} i_c = {{\dfrac{\varepsilon}{r}}} &\Rightarrow& 20 = {{\dfrac{1,5}{r}}} &\therefore& r = 0,075 \ \Omega \end{matrix}Dessa forma, a corrente que percorre o circuito é: \begin{matrix} \varepsilon = (2R + R_L + r)i &\therefore& i \approx 3,35 \ \pu{A} \end{matrix}Portanto, a potência dissipada pela lâmpada: \begin{matrix} Pot_L =R_L \cdot i^2 &\therefore& \fbox{$ Pot_L \approx 3,7 \ W $} \end{matrix}\begin{matrix} Letra \ (A) \end{matrix}