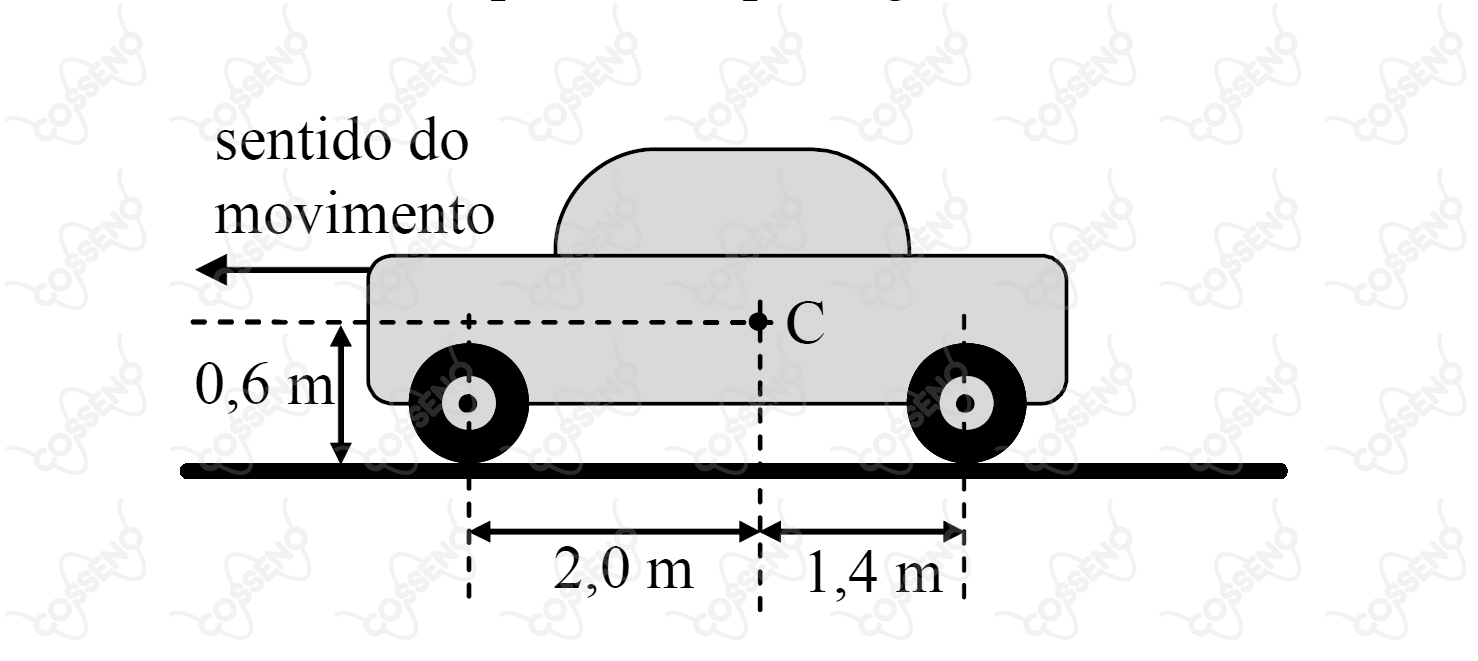
Considere um automóvel de peso , com tração nas rodas dianteiras, cuja centro de massa está em , movimentando-se num plano horizontal. Considerando , calcule a aceleração máxima que o automóvel pode atingir, sendo o coeficiente de atrito entre os pneus e o piso igual a .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Antes de começar a fazer contas, vale lembrar que a força de atrito atua no sentido contrário ao deslizamento entre as superfícies. Portanto, teremos uma força de atrito na roda dianteira atuando no sentido do movimento.
Fazendo somatório dos torques em relação ao centro de massa igual a zero.
$$2 \vert \vec{N_{1}} \vert - 1,4 \vert \vec{N_{2}} \vert + \vert \vec{f_{at}} \vert = 0 \\
2N_{1} - 1,4N_{2} + (0,75N_{1})0,6 = 0 \\
N_{2} = \dfrac{2,45N_{1}}{1,4}.$$
Fazendo somatório de forças na vertical igual a zero.
$$\vert \vec{N_{1}} \vert + \vert \vec{N_{2}} \vert = \vert \vec{P} \vert \\
P = \dfrac{3,85N_{1}}{1,4}.$$
Por fim, aplicando a segunda lei de Newton, obtemos que
$$f_{at} = ma \Rightarrow \dfrac{P}{g}a = \mu \dfrac{1,4P}{3,85} \Rightarrow a \approx 2,7 m/s^{2}.$$

