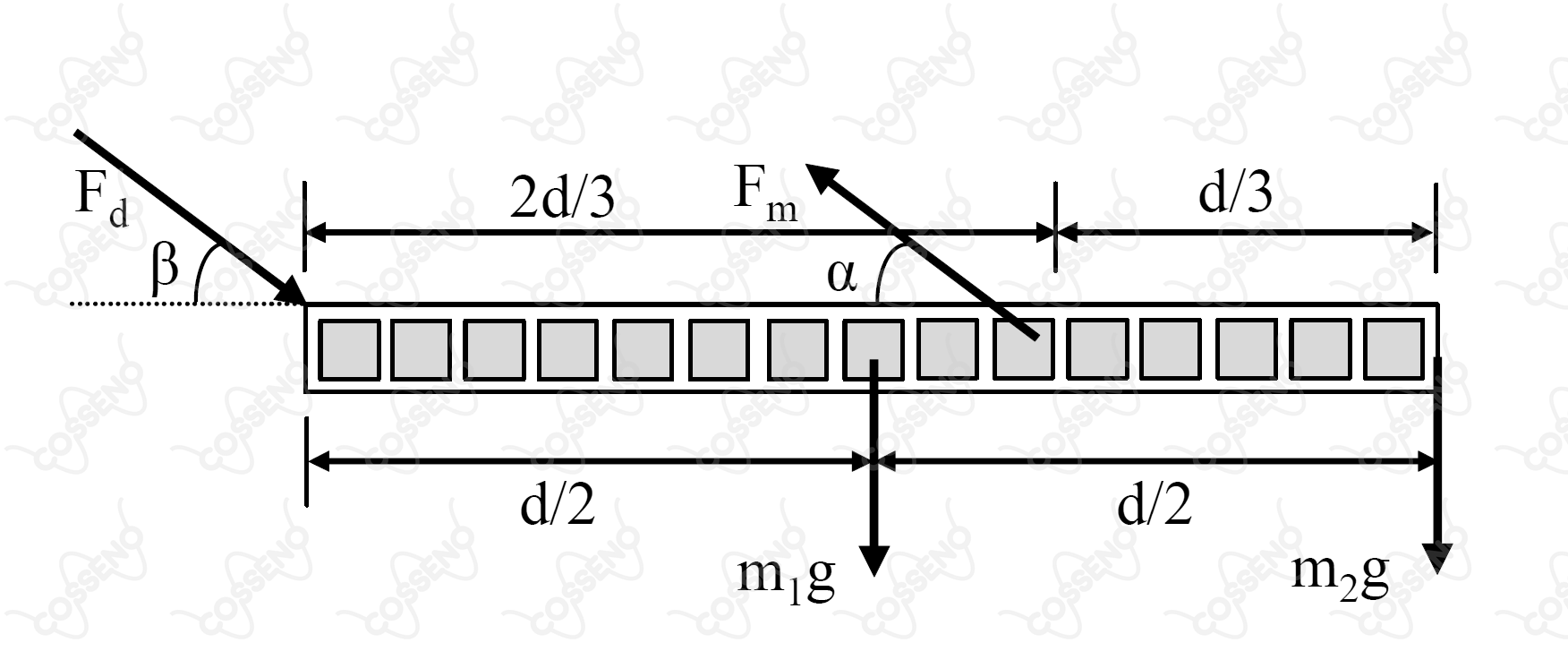
Considere uma pessoa de massa m que ao curvar-se permaneça com a coluna vertebral praticamente nivelada em relação ao solo. Sejam massa do tronco e soma das massas da cabeça e dos braços. Considere a coluna como uma estrutura rígida e que a resultante das forças aplicadas pelos músculos à coluna seja e que seja a resultante das outras forças aplicadas à coluna, de forma a mantê-la em equilíbrio. Qual é o valor da força ?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$1)$ Fazendo somatório dos torques no ponto que atua a força $F_{d}$.
$$\dfrac{mgd}{5} - \dfrac{2dF_{M} \sin \alpha}{3} + \dfrac{mgd}{5} = 0 \Rightarrow \\
\Rightarrow F_{M} = \dfrac{3mg}{5 \sin \alpha}.$$
$2)$ Fazendo somatório dos torques em relação ao ponto que atua a força $F_{M}$.
$$\dfrac{2d F_{d} \sin \beta}{3} + \dfrac{mgd}{15} - \dfrac{mgd}{15} = 0 \Rightarrow \\
\Rightarrow F_{d} \sin \beta = 0.$$
Como a força $F_{d} \neq 0$, então $\sin \beta = 0$, portanto $\beta = 0^\circ$. Então $F_{d} = F_{M} cos \alpha.$ Mas, perceba que já temos o módulo de $F_{M}$, portanto
$$F_{d} = \dfrac{3mg \cot \alpha}{5}.$$
Para encontrar o valor que consta no gabarito, use a relação fundamental da trigonometria.
$$\sin^{2} \alpha + \cos^{2} \alpha = 1 \Rightarrow \dfrac{9m^{2}g^{2}}{25F_{M}^{2}} + \dfrac{F_{d}^{2}}{F_{M}^{2}} = 1 \Rightarrow \\
\Rightarrow \vert \vec{F_{d}} \vert = \dfrac{\sqrt{25 \vert \vec{F_{M}} \vert^{2} - 9m^{2}g^{2}}}{5}.$$
Para aprender mais sobre equilíbrio de Torques, recomendo a leitura do capítulo 2 do livro do David Morin.

