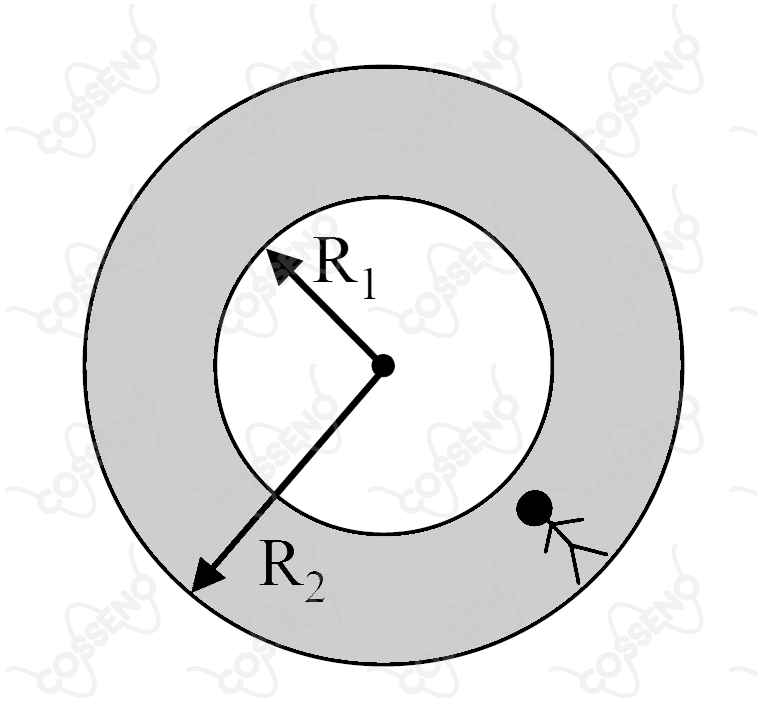
Uma estação espacial em forma de um toróide, de raio interno , e externo , gira, com período , em torno do seu eixo central, numa região de gravidade nula. O astronauta sente que seu “peso” aumenta de , quando corre com velocidade constante no interior desta estação, ao longo de sua maior circunferência, conforme mostra a figura. Assinale a expressão que indica o módulo dessa velocidade.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pesando na situação inicial, isto é, aquela em que o astronauta está parado em relação a estação, tem-se a partir do período a velocidade:\begin{matrix}
P = \dfrac{2\pi R_2}{u} &\Rightarrow& u = \dfrac{2\pi R_2}{P}
\end{matrix}Observe que o "peso" é responsabilidade da força centrífuga que atua sobre o astronauta, ou seja, em primeiro momento:\begin{matrix}
F_{cf_1} = \dfrac{mu^2}{R_2}
\end{matrix}Por outro lado, conforme o astronauta corre no interior da estação, a velocidade escalar é acrescida de $v$, resultando numa nova força centrífuga:\begin{matrix}
F_{cf_2} = \dfrac{m(u+v)^2}{R_2}
\end{matrix}Segundo enunciado, as forças se correlacionam a partir de um aumento de $20\%$, isto é :\begin{matrix}
F_{cf_2} = 1,2 F_{cf_1}
\end{matrix}Portanto, substituindo os resultados encontrados:\begin{matrix}
\dfrac{m(u+v)^2}{R_2} = 1,2\left( \dfrac{mu^2}{R_2} \right)\\ \\
(u+v)^2 = 1,2u^2 \\ \\
v = u(\sqrt{1,2} - 1) \\ \\
\boxed{v = \left( \sqrt{\dfrac{6}{5}} - 1\right) \dfrac{2\pi R_2}{P}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}
Adote um referencial inercial externo para a análise.
No caso $1$ tem-se que o astronauta está em repouso em relação a estação espacial , temos que a força $F_{c_{1}}$ que ele sente é dada por $F_{c_{1}} = \dfrac{mv_{1}^2}{R_{2}}$ , em que $v_{1}$ é a velocidade do astronauta(para o referencial adotado).
No caso $2$ é acrescentado uma velocidade $v$ à velocidade $v_{x}$ do astronauta devido ao fato de o astronauta começar a correr , nesse caso a força que ele sente é dada por $F_{c_{2}} = \dfrac{m(v_{1} + v)^2}{R_{2}}$ , pelo enunciado podemos constatar que
$F_{c_{2}} =\dfrac{120}{100} \cdot F_{c_{1}} $
$\therefore$
$ \dfrac{m(v_{1} + v)^2}{R_{2}} =\dfrac{6}{5}\cdot \dfrac{mv_{1}^2}{R_{2}} $
$\implies v = \left(\sqrt{\dfrac{6}{5}} - 1\right)v_{1}$
temos que $v_{1} = \omega_{1} \cdot R_{2} = \dfrac{2\pi \cdot R_{2}}{P}$
$\therefore$
$\boxed{v = \left(\sqrt{\dfrac{6}{5}} - 1\right)\dfrac{2\pi \cdot R_{2}}{P}}$


