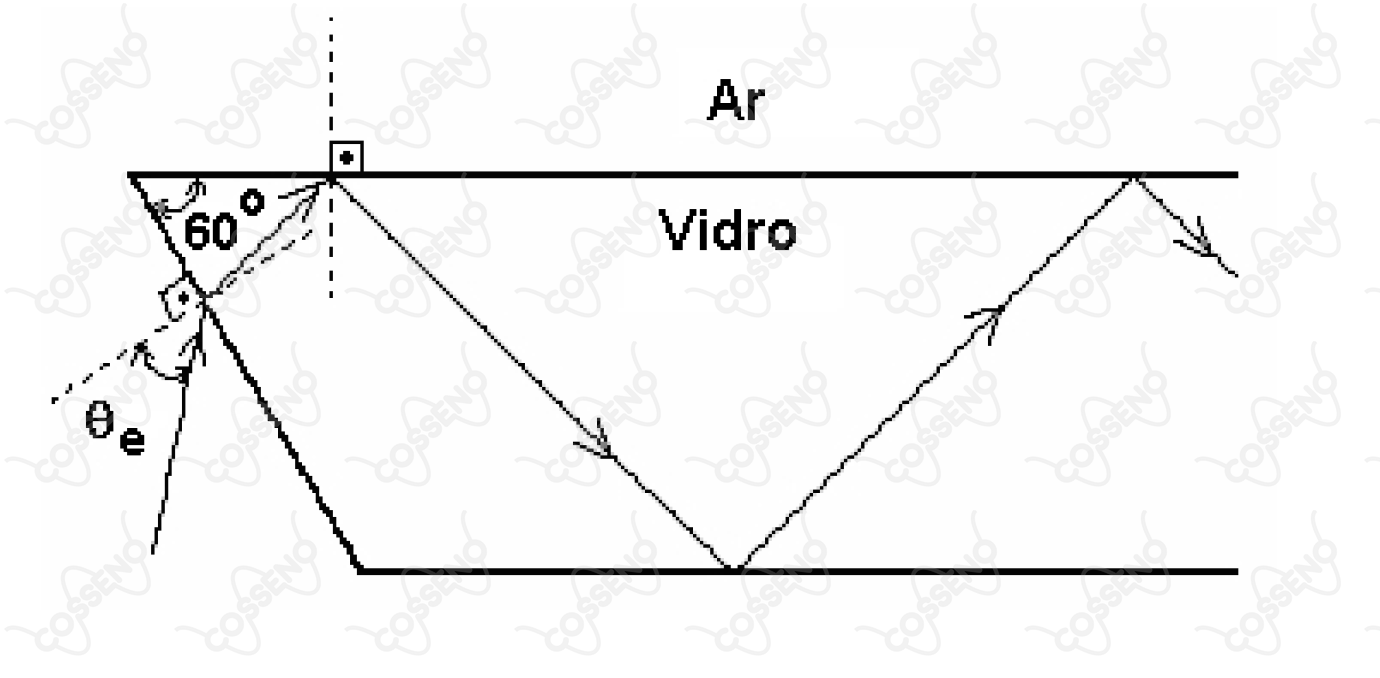
A figura mostra uma placa de vidro com índice de refração mergulhada no ar, cujo índice de refração é igual a . Para que um feixe de luz monocromática se propague pelo interior do vidro através de sucessivas reflexões totais, o seno do ângulo de entrada, e deverá ser menor ou igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Esboçando a situação a fim de elucidar melhor a imagem:
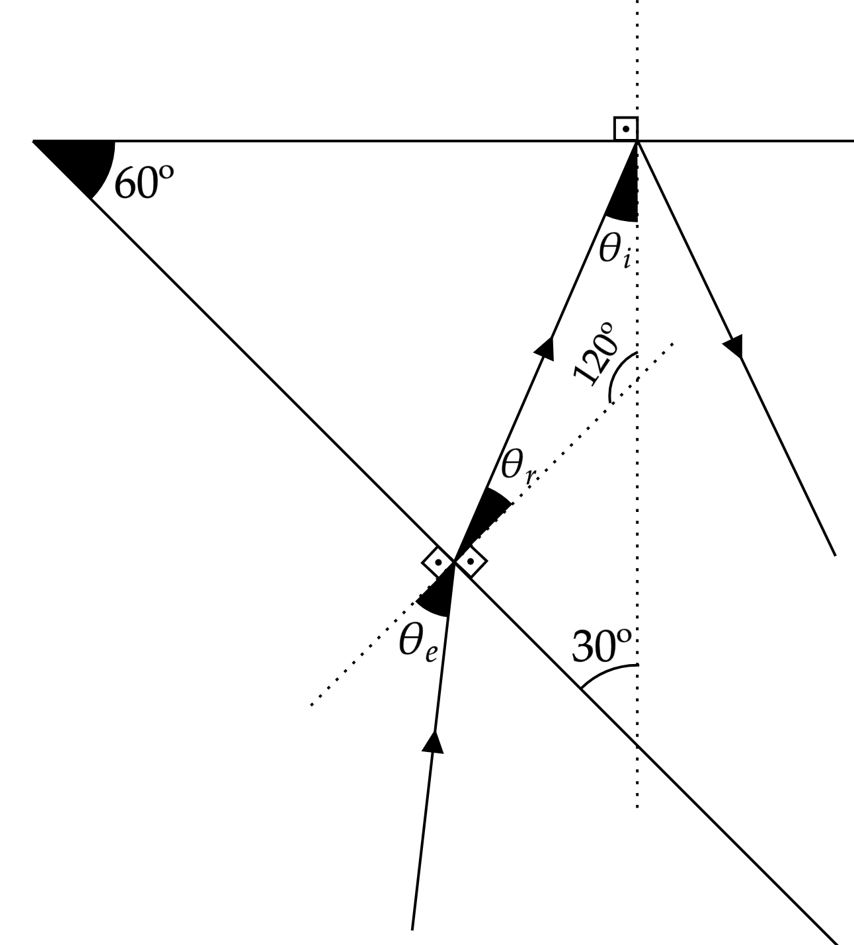Para reflexão total:\begin{matrix}
\dfrac{\sin{\theta_i}}{\sin{90º}} = \dfrac{n_{ar}}{n_v} &\Rightarrow& \sin{\theta_i} =\dfrac{\sqrt{2}}{2} &\therefore& \boxed{\theta_i = 45º}
\end{matrix}Analisando a geometria do problema:\begin{matrix}
\theta_r + \theta_i + 120º = 180º \\ \boxed{\theta_r = 15º }
\end{matrix}Novamente, aplicando a lei de Snell:\begin{matrix}\dfrac{\sin{\theta_e}}{\sin{\theta_r}} = \dfrac{n_{v}}{n_{ar}} &\Rightarrow& \sin{\theta_e} = \sqrt{2}\cdot \sin{15º}
\end{matrix}É necessário ter conhecimento do $\sin{15º}$, ou ao menos saber encontrá-lo. No caso, podemos fazer:\begin{matrix}
\sin{(60º - 45º)} = \sin{60º}\cos{45º} - \sin{45º}\cos{60º}
\end{matrix}\begin{matrix}
\boxed{\sin{15º} = \dfrac{\sqrt{6} - \sqrt{2}}{4}}
\end{matrix}Substituindo no resultado anterior:\begin{matrix}
\sin{\theta_e} = \dfrac{\sqrt{3} - 1}{2} &\therefore&\boxed{\sin{\theta_e} \approx 0,37}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}$\color{orangered}{\text{Obs:}}$ $\sqrt{3} \approx 1,73$
Ampliar Imagem
