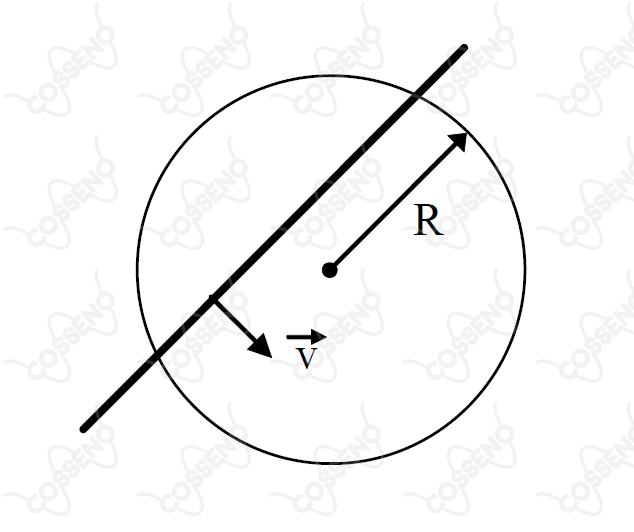
Um fio delgado e rígido, de comprimento , desliza, sem atrito, com velocidade sobre um anel de raio , numa região de campo magnético constante . Pode-se, então, afirmar que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Primeiro, vamos pensar na direção de $\vec{B}$: com o campo magnético paralelo ao plano do anel, não haverá fluxo magnético $(\vec{B}\cdot\vec{A}=0)$. Assim, a alternativa (C) está incorreta.
Com o campo magnético perpendicular ao plano do anel haverá fluxo, mas sendo o fio isolante elétrico, não haverá nenhuma força que possa fazê-lo parar. Assim, as alternativas (B) e (E) estão erradas.
Resta agora analisar as alternativas (A) e (E): será que, com materiais condutores e $\vec{B}$ perpendicular ao plano do anel, pode haver uma força que pare o fio, ou a ação do campo magnético não afeta o movimento do fio nesse eixo - fazendo com que ele siga em frente pela lei da inércia?
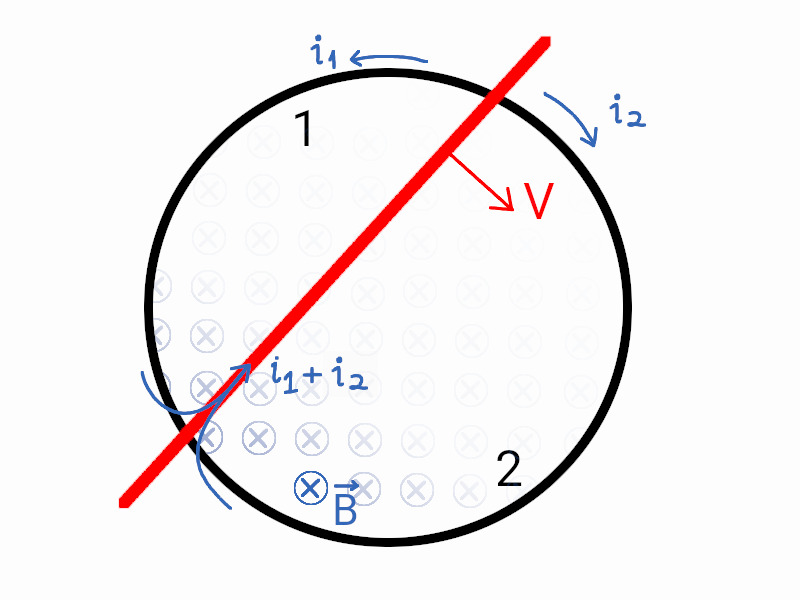 Olhando para a seção $1$, conforme o fio se move a área da seção aumenta, provocando uma variação de fluxo magnético. De acordo com a lei de Faraday-Lenz, surgirá uma corrente no anel para opor a variação de fluxo. O sentido dessa corrente $i_1$, dado pela regra da mão direita, foi desenhado acima.
O mesmo vale para a seção $2$. Com a regra da mão direita, podemos desenhar o sentido da corrente $i_2$.
Portanto, a corrente "resultante" $i$ que vai percorrer o fio é dada pela soma das correntes das seções: $i = i_1 + i_2$. Dessa forma, a força eletromotriz associada a essa corrente tem sentido dado pela regra da mão direita, contrariando o movimento do fio.
Provamos que é possível haver uma situação na qual o fio para, fazendo com que a alternativa (A) esteja incorreta. $\boxed{\text{Gab. D)}}$
Olhando para a seção $1$, conforme o fio se move a área da seção aumenta, provocando uma variação de fluxo magnético. De acordo com a lei de Faraday-Lenz, surgirá uma corrente no anel para opor a variação de fluxo. O sentido dessa corrente $i_1$, dado pela regra da mão direita, foi desenhado acima.
O mesmo vale para a seção $2$. Com a regra da mão direita, podemos desenhar o sentido da corrente $i_2$.
Portanto, a corrente "resultante" $i$ que vai percorrer o fio é dada pela soma das correntes das seções: $i = i_1 + i_2$. Dessa forma, a força eletromotriz associada a essa corrente tem sentido dado pela regra da mão direita, contrariando o movimento do fio.
Provamos que é possível haver uma situação na qual o fio para, fazendo com que a alternativa (A) esteja incorreta. $\boxed{\text{Gab. D)}}$

Ampliar Imagem

