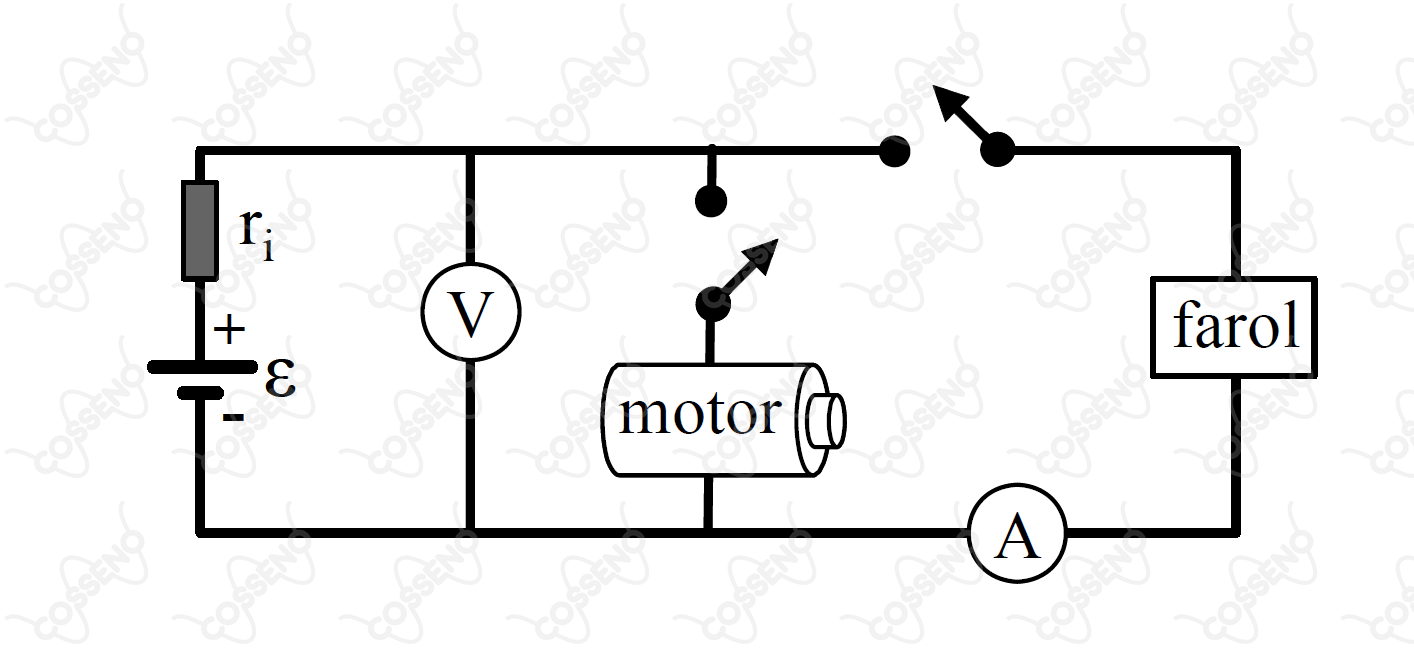
Quando se acendem os faróis de um carro cuja bateria possui resistência interna , um amperímetro indica uma corrente de e um voltímetro uma voltagem de . Considere desprezível a resistência interna do amperímetro. Ao ligar o motor de arranque, observa-se que a leitura do amperímetro é de e que as luzes diminuem um pouco de intensidade. Calcular a corrente que passa pelo motor de arranque quando os faróis estão acesos.
Na situação inicial, fechamos a chave de cima do circuito para ligar o farol, assim, a partir dos dados do enunciado, é possível encontrar a resistência $(R)$ desse farol, veja: \begin{matrix} 12= R \ . 10 &\therefore& R = 1,2 \ \Omega
\end{matrix}Além disso, pode-se encontrar a $fme$ do circuito: \begin{matrix} 12 = \varepsilon - 0,05.10 &\therefore& \varepsilon = 12,5 \ V
\end{matrix}Agora, ao ligar o motor, sabemos que passa uma corrente de $8,0 \ A$ no farol, com isso, a nova $ddp$ será: \begin{matrix} \Delta V = 1,2 \ . 8 &\therefore& \Delta V = 9,6 \ V
\end{matrix}Nessa perspectiva, já é possível achar a corrente que sai da bateria: \begin{matrix} \Delta V = \varepsilon - r.i &\Rightarrow& 9,6 = 12,5 - 0,05.i &\therefore& i = 58 \ A
\end{matrix}Segundo as $\text{Leis de Kirchhoff}$, a corrente $i_M$ que vai para o motor, e a corrente $i_F$ que vai para o farol são relacionadas como: \begin{matrix} i = i_M + i_F &\Rightarrow& 58 = i_M + 8 &\therefore& \fbox{$ i_M = 50 \ A $}
\end{matrix}
