A priori, podemos pensar na relação fundamental de uma elipse e escrever:\begin{matrix} \overline{F_1A} + \overline{F_1A} = 2a \\ \sqrt{(0-0)^2 + (9-6)^2} + \sqrt{(0-0)^2 + (9+6)^2} = 2a \\ \boxed{a = 9} \end{matrix}Nesse contexto, nota-se que $A$ é uma extremidade do eixo vertical da elipse, inclusive, eixo esse o maior. Dessa forma, vamos tentar esboçar a situação: 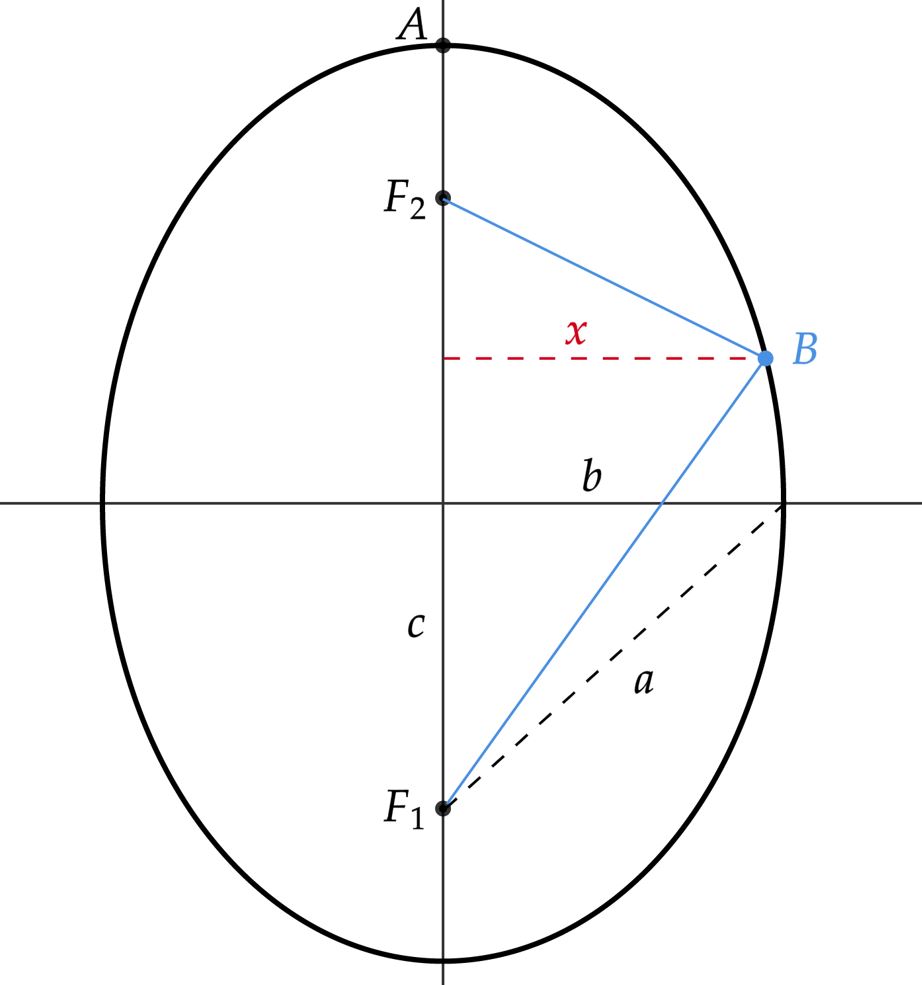Pensando na equação da elipse, podemos escrever:\begin{matrix} \dfrac{x^2}{b^2} + \dfrac{y^2}{9^2} = 1 \end{matrix}Em busca do valor de $b$, pode-se usar a relação pitagórica da elipse:\begin{matrix} a^2 = b^2 + c^2 &,& c = 6 &\therefore& \boxed{b = 3\sqrt{5} } \end{matrix}Substituindo o nosso resultado acima na equação da elipse no intuito de encontrar o pono $x$ de $B$, constata-se:\begin{matrix} \dfrac{x^2}{( 3\sqrt{5})^2} + \dfrac{3^2}{9^2} = 1 &\Rightarrow& x^2 =40 &\therefore& |x| = 2\sqrt{10} \end{matrix}Por fim, resta apenas encontrar a área do triângulo, tal que:\begin{matrix} \ce{[BF_1F_2]} = \dfrac{|x|(2c)}{2} =12\sqrt{10} &\tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (D) \end{matrix}