Pensando num cone circular reto, pode-se esboçar: 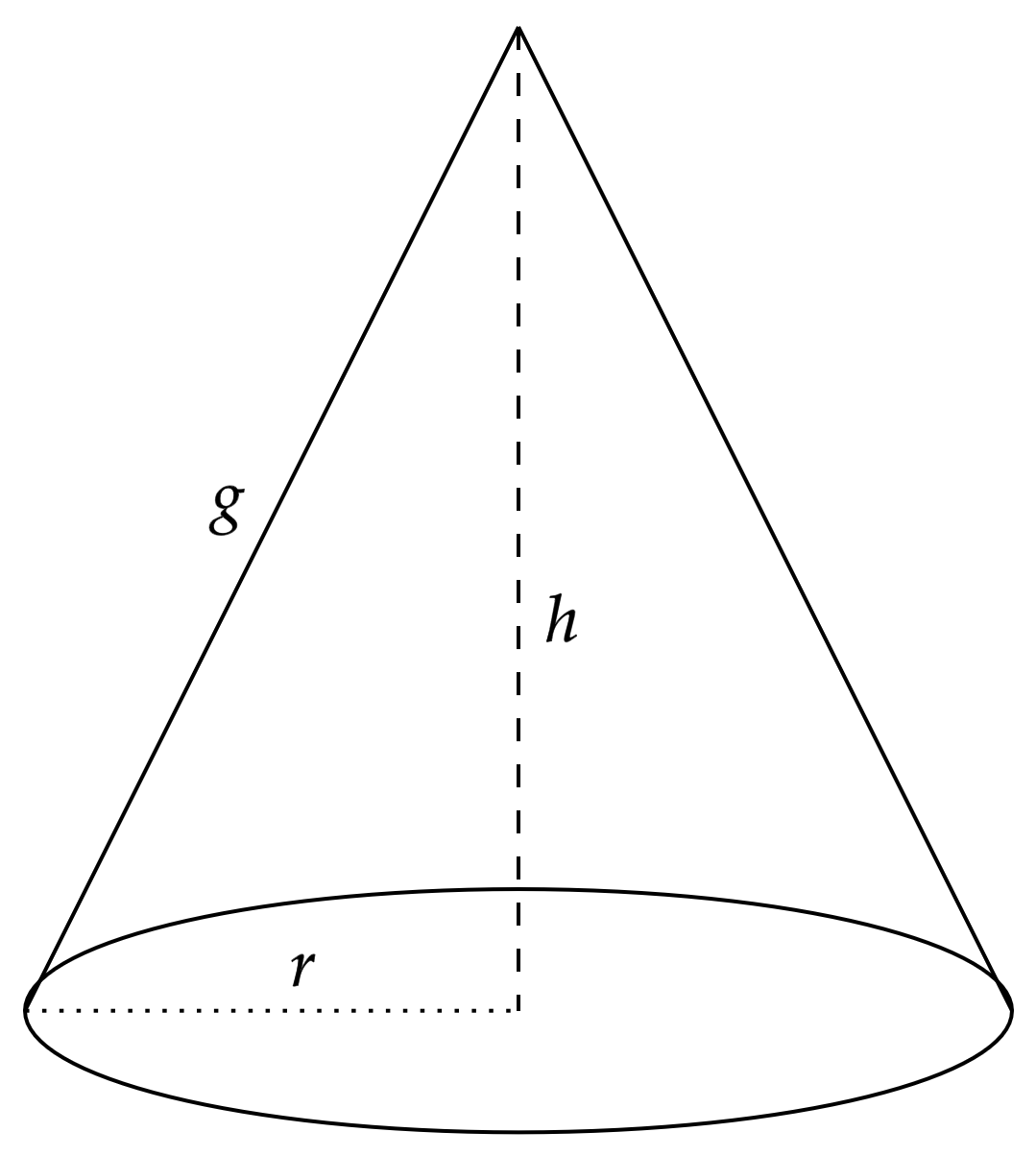Conforme teorema de Pitágoras, têm-se:\begin{matrix} g^2 = h^2 + r^2 \end{matrix}Visto que $r$, $h$ e $g$ estão em uma progressão aritmética, segue que:\begin{matrix} (h+2)^2 = h^2 + (h-2)^2 &\Rightarrow& h= 8 \ \pu{m}&\therefore& \begin{cases} r = 6 \ \pu{m} \\ g = 10 \ \pu{m} \end{cases} \end{matrix}Agora, resta-nos encontrar a área total, isto é:\begin{matrix} A_{total} = A_{base} + A_{lateral} \end{matrix}Em que,\begin{matrix} A_{base} = \pi r^2 &,& A_{lateral} =\pi gr \end{matrix}Consequentemente,\begin{matrix} A_{total} = \pi r(r + g) &\therefore& A_{total} = 96\pi \ \pu{m2} \ \ \tiny{\blacksquare} \end{matrix}