Pensando numa pirâmide regular de base hexagonal, têm-se algo como: 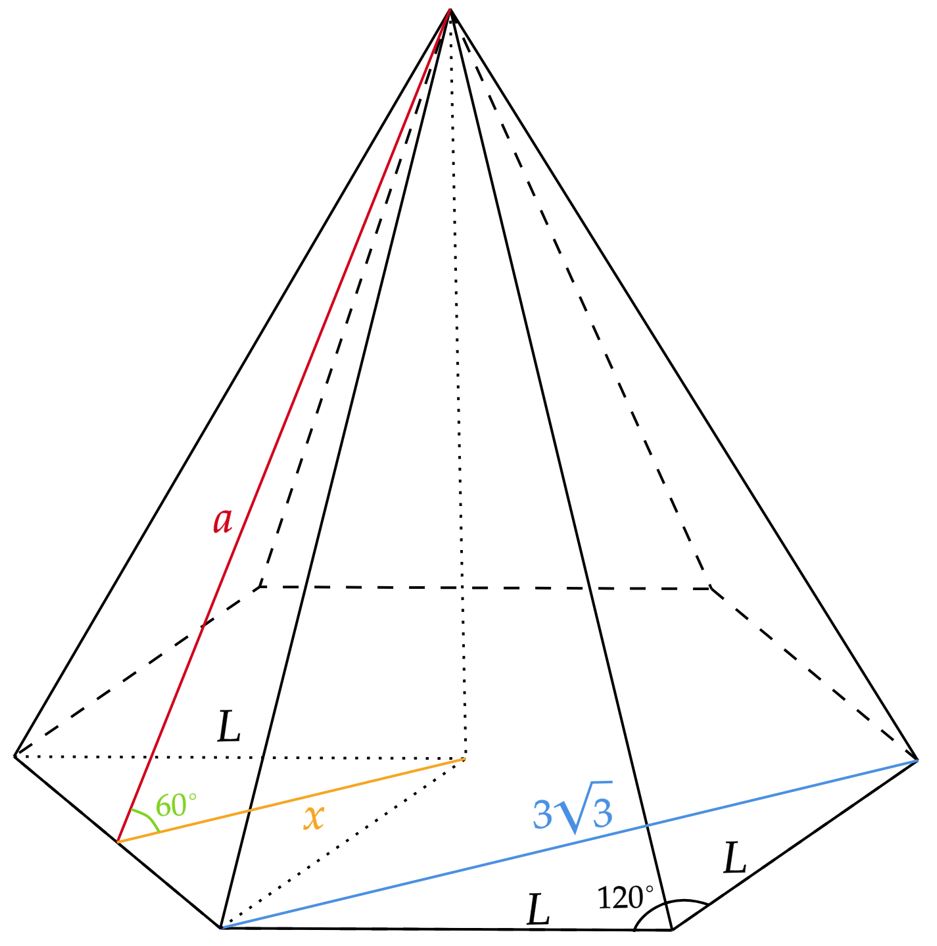Começando pela aresta $L$, podemos encontrá-la a partir da lei dos cossenos, veja: \begin{matrix} (3\sqrt{3})^2=L^2+L^2−2⋅L⋅L\cos{120^∘} &\therefore &L=3 \ \pu{cm} \end{matrix}Agora, perceba que o apótema da base $(x)$ é igual a altura de um triângulo equilátero de lado $L$, assim: \begin{matrix} x = {{\dfrac{L\sqrt{3}}{2} }} &\therefore& x = {{\dfrac{3\sqrt{3}}{2} }} \ \pu{cm}\end{matrix}Continuando, pelo ângulo formado entre o apótema da base e o apótema da pirâmide, têm-se: \begin{matrix} \cos{60^∘} = {{\dfrac{x}{a} }} &\Rightarrow& a = 2x &\therefore& a = 3\sqrt{3}\end{matrix}Por fim, a área total da pirâmide: \begin{matrix} A_{Total}=A_{Base}+A_{Faces} &\Rightarrow& A_{Total}=6⋅{{(\dfrac{L^2\sqrt{3}}{4})}}^2 + 6⋅{{(\dfrac{L \cdot a}{2})}} &∴&A_{Total}= {{\dfrac{81\sqrt{3}}{2}}} \ \pu{cm^2} & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (A) \end{matrix}