São de e , respectivamente, as frequências de duas harmônicas adjacentes de uma onda estacionária no trecho horizontal de um cabo esticado, de comprimento e densidade linear de massa igual a (veja figura).
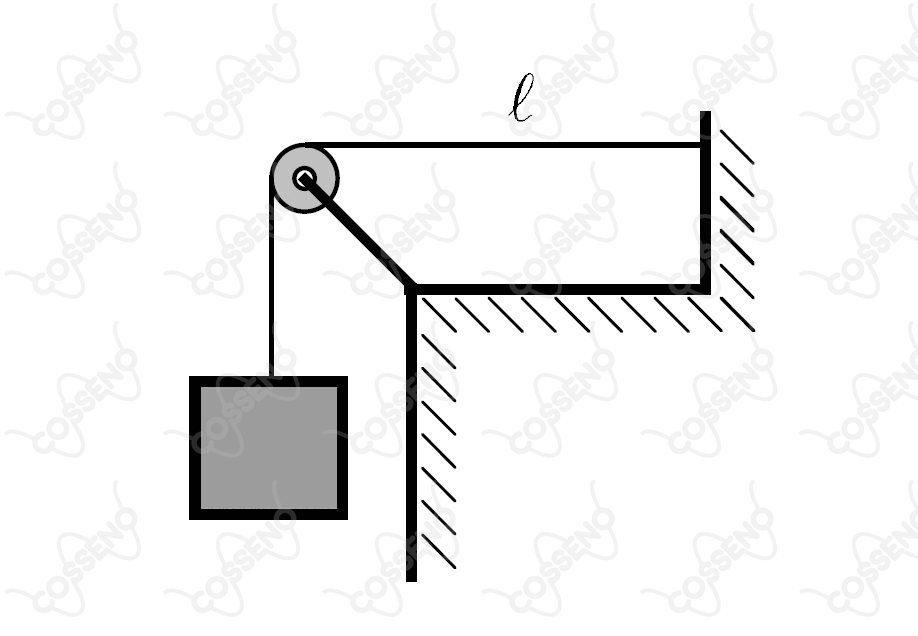
Considerando a aceleração da gravidade , a massa do bloco suspenso deve ser de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, podemos analisar o equilíbrio do bloco, tal que:\begin{matrix}T = mg
\end{matrix}Visando encontrar a tração, podemos utilizar a equação de Taylor:\begin{matrix}
v = \sqrt{\dfrac{T}{\mu}} &\Rightarrow& T = \mu v^2 &\text{(I)}
\end{matrix}Veja que o enunciado nos fornece a densidade linear de massa, assim, resta encontrar a velocidade da corda. Nessa perspectiva, vamos pensar em dois harmônicos adjacentes, em que:\begin{matrix} l = n \left(\dfrac{\lambda}{2} \right)&,& l = (n+1) \left(\dfrac{\lambda}{2} \right)
\end{matrix}Conforme equação fundamental da ondulatória, têm-se:\begin{matrix}
l = n \left(\dfrac{v}{2f_1} \right)&,& l = (n+1) \left(\dfrac{v}{2f_2} \right) \\ \\
n = \dfrac{2l f_1}{v} &&n+1 = \dfrac{2l f_2}{v}
\end{matrix}Com isso,\begin{matrix}v =2l(f_2 - f_1) &\therefore& v = 100 \ \pu{m/s}
\end{matrix}Substituindo o resultado acima em $\text{(I)}$ e logo em seguida da equação do equilíbrio:\begin{matrix}mg = 10(100)^2 &\Rightarrow&m = 100^2 \ \pu{g} &\therefore& \boxed{m = 10 \ \pu{kg}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}

