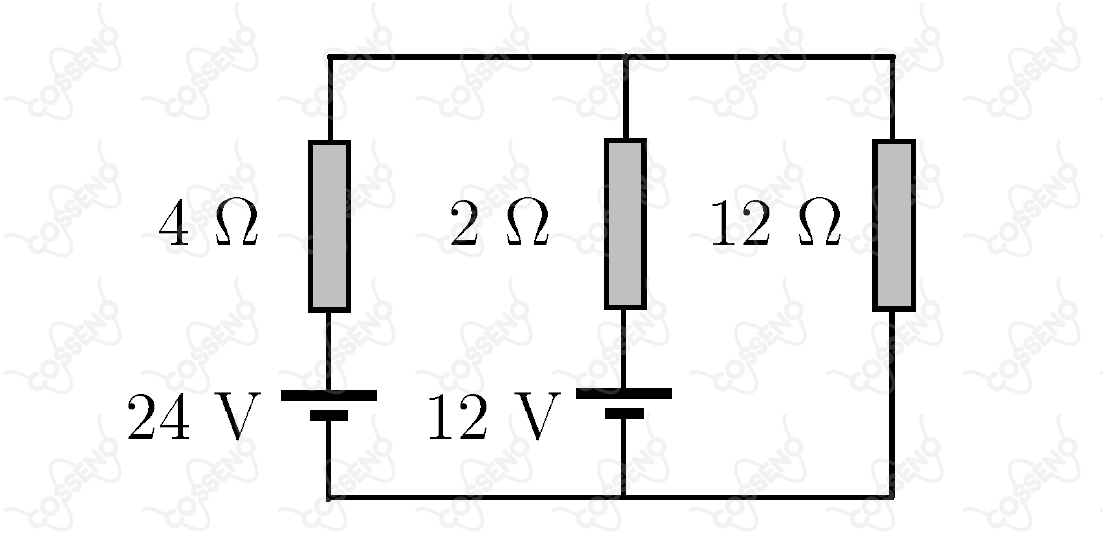
Um técnico em eletrônica deseja medir a corrente que passa pelo resistor de no circuito da figura. Para tanto, ele dispõe apenas de um galvanômetro e uma caixa de resistores. O galvanômetro possui resistência interna e suporta, no máximo, uma corrente de . Determine o valor máximo do resistor a ser colocado em paralelo com o galvanômetro para que o técnico consiga medir a corrente.
CossenoGPT
Teste
gratuitamente agora
mesmo! 
A priori, é interessante encontrar um gerador equivalente, pois facilitará as contas, assim, comecemos com: \begin{matrix} {{\dfrac{\varepsilon}{R_{eq}}}} = {{\dfrac{24}{4}}} + {{\dfrac{12}{2}}} &,& {{\dfrac{1}{R_{eq}}}} = {{\dfrac{1}{4}}} + {{\dfrac{1}{2}}} &\Rightarrow& R_{eq} = {{\dfrac{4}{3}}} \ \Omega &,& \varepsilon = 16 \ V
\end{matrix}Dessa forma, redesenhando o circuito, temos:
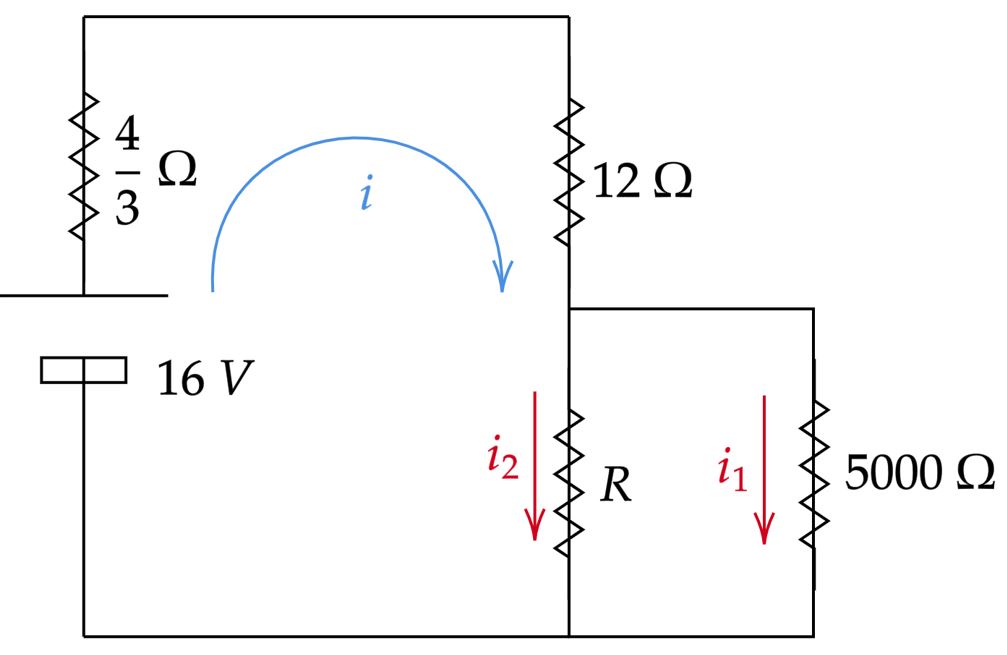$-$ Aplicando as $\text{Leis de Kirchhoff}$: \begin{matrix} {{\dfrac{4}{3}}}i + 12i + Ri_2 = 16 &,& Ri_2 = 5000\cdot i_1 &,& i = i_1 + i_2
\end{matrix}Note que, segundo enunciado, pede-se o valor máximo do resistor $R$, logo, $\color{royalblue}{i_1 = 0,1 \cdot 10^{-3} \ \pu{A}}$ , então,\begin{matrix} Ri_2 = 0,5 &\Rightarrow& i = {{\dfrac{93}{80}}} &\therefore& i_2 \approx i
\end{matrix}Continuando, \begin{matrix} R\cdot {{\dfrac{93}{80}}} = 0,5 &\therefore& &\fbox{$R \approx 0,43 \ \Omega$}&
\end{matrix}
Ampliar Imagem
