Em uma impressora a jato de tinta, gotas de certo tamanho são ejetadas de um pulverizador em movimento, passam por uma unidade eletrostática onde perdem alguns elétrons, adquirindo uma carga , e, a seguir, se deslocam no espaço entre placas planas paralelas eletricamente carregadas, pouco antes da impressão. Considere gotas de raio igual a lançadas com velocidade de modulo entre placas de comprimento igual a , no interior das quais existe um campo elétrico vertical uniforme, cujo módulo é (veja figura).
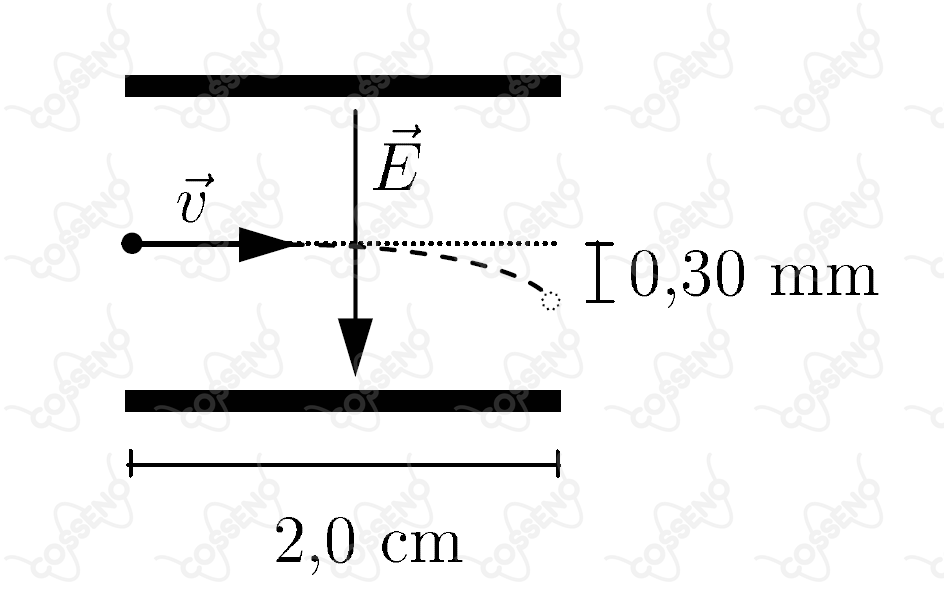
Considerando que a densidade da gota seja de e sabendo-se que a mesma sofre um desvio de ao atingir o final do percurso, o módulo da sua carga elétrica é de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Conforme a figura, é possível obter a seguinte relação:
$$ F_{r} = |F_{el}| \ \Rightarrow \ ma = qE \ \Rightarrow \ a = \dfrac{qE}{m} \ (I)$$
Portanto, precisamos encontrar a aceleração da partícula na vertical, sua massa, assim o exercício estará resolvido. Perceba que o enunciado fornece a densidade da gota e seu raio, logo:
$$d = \dfrac{m}{V} \ \Rightarrow \ m = d \cdot \frac{4}{3}\pi r^{3} \Rightarrow \ m \approx 4,0 \cdot 10^{-4}kg $$
Agora, basta aplicar a equação do movimento uniforme no eixo horizontal e movimento uniformemente variado no eixo vertical.
$$x: x = x_{0} + vt \ \Rightarrow \ t = \dfrac{2,0 \cdot 10^{-2}}{20} = 1,0 \cdot 10^{-3}s$$
$$y: y = y_{0} + v_{0}t + \frac{1}{2}at^{2} \ \Rightarrow \ a = 6,0 \cdot 10^{2}m/s^{2} $$
Voltando na equação $(I)$ e subtituindo os valores, encontramos
$$\boxed{q = 3,1 \cdot 10^{-14}C}$$

